Objetivos de la clase
- Ilustrará mediante ejemplos y definiciones su comprensión de los términos brazo de palanca y momento de torsión.
- Calculará el momento de torsión resultante respecto a cualquier eje, dadas las magnitudes y posiciones de las fuerzas que actúan sobre un objeto alargado
- Determinará las fuerzas o distancias desconocidas aplicando la primera y segunda condiciones de equilibrio
- Definirá centro de gravedad y dará ejemplos de dicho concepto
Las fuerzas son las que determinan el movimiento de los cuerpos, si la fuerza neta es distinta de cero, el objeto sobre el cual actúan estas fuerzas comenzará a cambiar su estado de movimiento, (acelerando). Pero si la suma de fuerzas es cero, entonces el cuerpo permanecerá en reposo o bien se moverá con velocidad constante.
pero a esta última condición existe la siguiente situación.
podemos notar que si F1 y F2 son iguales en magnitud, el cuerpo no se quedará en reposo, sino que comnezará a girar, cuando se tiene esta situación, hablamos de torques
Desarrollo
Un torque es aquello que provoca el giro de los cuerpos, de manera que si un cuerpo está en reposo, al aplicar un torque podemos hacer que comience a girar, o si un cuerpo ya está girando con el torque adecuado podemos hacer que deje de girar.
y si un cuerpo no gira, pudiendo hacerlo, podemos decir que la suma de torques que actúan sobre el es cero, de la misma manera como se define la primera ley de Newton ...
Operacionalmente un torque se calcula así ...
Tau, es la letra para identificar el torque
F es la fuerza aplicada
d es el brazo de palanca
el símbolo x, es el producto cruz, equivale al producto vectorial de vectores, ya que cuando se multiplican vectores, se pude usar el producto punto o el producto cruz.
En el caso de los torques el producto cruz, equivale a multiplicar el módulo de F, por le módulo de d por el seno del ángulo que se forma entre F y d.
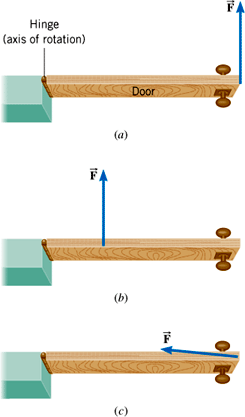
La figura muestra una puerta y tres fuerzas aplicadas a la puerta, en los casos a y b, la puerta girará fácilmente, y en el caso a será más fácil hacerla girar que en el caso b, pero en el caso c, si la fuerza está dirigida en la misma dirección que la hoja de la puerta, ¿habrá giro?
La fuerza aplicada, a un objeto que puede girar, hará torque sólo si tiene alguna componente que sea perpendicular al brazo de palanca del objeto.
el brazo de palanca es la distancia medida desde el punto en donde el objeto puede girar hasta el punto en donde se aplica la fuerza.
por lo tanto las fuerzas paralelas (o antiparalelas) al brazo de palanca no producen torque.
y si la fuerza aplicada es perpendicular al brazo de palanca entonces el torque aplicado por esta fuerza es máximo. (ya que sen 90º = 1)
En la siguiente figura, cuáles son los torques de la niña del niño.
La razón es que, para que exista equilibrio, la suma de los torques externos debe ser cero, para que esta suma sea cero, vamos a fijarnos en el tipo de giro que provocan los torques
un giro en dirección horaria tendrá signo negativo
y un giro en dirección antihoraria tendrá signo positivo
(igual como se miden los ángulos en un sistema de coordenadas x e y)
entonces de acuerdo con estas definiciones, el torque del niño es negativo, ya que si sólo estuviera el niño sobre la barra del balancín, este se movería en dirección horaria, luego su torque es negativo ...
y en el caso de la niña, su torque es positivo, ya que si sólo estuviera la niña sobre la barra del balancín, este se movería en dirección antihoraria, luego su torque es positivo ...
así entonces se cumple la segunda condición de equilibrio.
Existen dos tipos de equilibrio:
El primer equilibrio, está relacionado con la primera ley de Newton, y se llama equilibrio traslacional, este equilibrio ocurre cuando la suma de fuerzas externas que actúan sobre un cuerpo es cero.
Por ejemplo:
El segundo equilibro se llama, equilibrio Rotacional, y este equilibro ocurre cuando la sumatoria de torques externos es cero.
En la figura, una persona sostiene una mancuerna. Su brazo está horizontal y pesa 31,0 N. Si suponemos que el único músculo que actúa es el deltoides y que está unido al brazo como se muestra en la figura. La fuerza máxima que el músculo deltoides puede suministrar tiene una magnitud de 1.840 N.
La figura muestra las distancias a las que se localizan las diversas fuerzas que actúan sobre el brazo.
¿Cuál es el peso de la mancuerna más pesada que se puede sostener?
y ¿cuáles son los componentes de la fuerza horizontal y vertical, que la articulación del hombro aplica al extremo izquierdo del brazo?
Sol
Wd = 86,1 N
Sx = 1790 N
Sy = -297 N (Notar el signo)
El centro de gravedad
El centro de gravedad de un cuerpo es el punto respecto al cual las fuerzas que la gravedad ejerce sobre los diferentes puntos materiales que constituyen el cuerpo producen un momento resultante nulo.
En la Figura una caja está apoyada cerca del extremo izquierdo de una tabla horizontal. El peso total actúa en el centro de gravedad del grupo. El grupo puede ser equilibrado mediante la aplicación de una fuerza externa (debido al dedo índice) en el centro de la gravedad.
Ejemplo:
Un sistema consiste de tres partículas ubicadas como muestra la figura, Halle el centro de masa del sistema.Sol:
xcm = 0,75 m
ycm = 1,0 m
El brazo horizontal ilustrado en la figura se compone de tres partes: la parte superior del brazo (W1 pesa 17 N), El brazo inferior (W2 = 11 N), Y la mano (W3 = 4,2 N). El dibujo muestra el centro de gravedad de cada parte, medido con respecto a la articulación del hombro. Encontrar el centro de gravedad de todo el brazo, con relación a la articulación del hombro.
Sol:
0,28 m
Cierre
- Torque
- Equilibro
- Rotacional
- Traslacional
- Centro de masa
Ejercicios Cromer
Ejercicios Jou