Objetivos de la clase
- Dinámica de fluidos, Bernoulli,
Inicio
Caudal
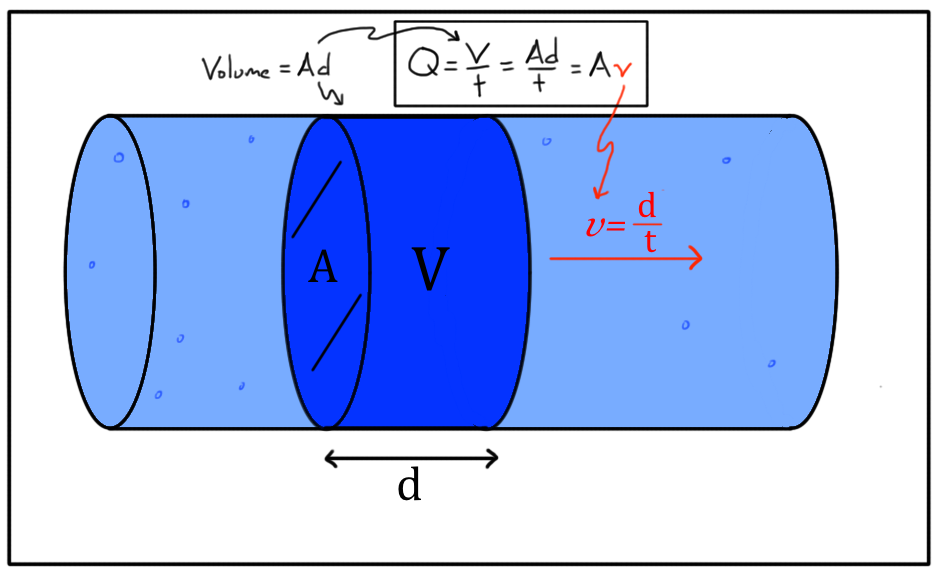
El caudal es la cantidad de fluido que circula por una tubería en un tiempo determinado, se puede calcular como ...
Q = (V)/(t)
si imaginamos el interior de una tubería, el volumen sería igual a
Q = (V)/(t) = (Ad)/(t) = A(d)/(t) = A·v
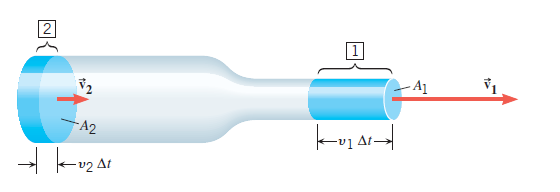
en una tubería la cantidad de fluido que ingresa a ella, debe ser la misma cantidad de fluido que sale de ella, a no ser que la tubería tenga pérdidas o ganancias de fluido. Si suponemos que no hay perdidas ni ganancias, entonces se cumple que el caudal es constante ...
Q1 = Q2
A1v1 = A2v2
Ecuación de continuidad

Ejemplo: Una manguera de jardín
Una manguera de jardín tiene su extremo abierto sin obstrucciones con un área de sección transversal de 2, 85 × 10 − 4m2, desde este extremo el agua llena un cubo en 30,0 s. El volumen del cubo es 8, 00 × 10 − 3m3 (aproximadamente dos galones). Encuentre la rapidez con que el agua sale de la manguera a través de (a) la abertura sin obstáculos y (b) una abertura obstruida con la mitad de su área.
Solución:
a) v = (Q)/(A) = ((8, 00 × 10 − 3m3)/(30, 0s))/(2, 85 × 10 − 4m2) = 0, 936m ⁄ s
b) v2 = (A1)/(A2)v1 = (A1)/((1)/(2)A1)0, 936m ⁄ s = 1, 87m ⁄ s
En la condición conocida como ateroesclerosis, un depósito, o ateroma, se forma sobre la pared arterial y reduce el lumen a través del cual puede fluir la sangre. En la arteraia carotida en el cuello, la sangre fluye tres veces más rápido a través de una región bloqueada que si lo hace por una región no obstruida. Halle la razón del radio efectivo de la arteria en los dos lugares.
Qno − obstruido = Qobstruido
Anovno = Aov0
πr2novno = πr2ovo
(rno)/(ro) = √((vo)/(vno)) = √(3) = 1, 7
Ecuación de Bernoulli
En un fluido estacionario, la rapidez, presión, y elevación de un fluido incompresible y no viscoso se relacionan mediante la ecuación de Daniel Bernoulli (1700-1782).
p + ρgh + (1)/(2)ρv2 = cte.
p1 + ρgh1 + (1)/(2)ρv21 = p2 + ρgh2 + (1)/(2)ρv22
ecuación de Bernoulli
viscosidad
Ley de Poiseuille