Sonido - Física con Zeuss

Física • 1° Medio • Primer Trimestre ⬅ Volver al trimestre

⬅ Anterior Unidad 2 de 3 Siguiente ➡ Menú principal

🔊 El Sonido

🎯 Objetivos de Aprendizaje

Discriminar sonidos de diferente altura, intensidad y timbre
Comprender los fenómenos de absorción, reflexión y transmisión del sonido
Reconocer estos fenómenos en la vida diaria

👂 El Oído Humano y la Percepción del Sonido

No todas las ondas sonoras pueden ser percibidas por el oído humano, el cual es sensible únicamente a aquellas cuya frecuencia está comprendida entre los 20 y los 20,000 Hz.

En el aire dichos valores extremos corresponden a longitudes de onda que van desde 16 metros hasta 1.6 centímetros respectivamente.

20 - 20,000 Hz

Rango de audición humana

🔬 Proceso de Audición

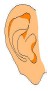
1. Tímpano: La onda sonora alcanza la membrana sensible del tímpano, produciendo vibraciones.

2. Cadena de huesecillos: Las vibraciones son transmitidas por la cadena de huesecillos hasta la ventana oval.

3. Amplificación: La ventana oval es 20 a 30 veces más pequeña que el tímpano, lo que amplifica la presión entre 40 y 90 veces.

4. Cóclea: La onda de presión se propaga a través de un líquido viscoso hasta alcanzar las fibras nerviosas.

5. Señales eléctricas: Las deformaciones elásticas estimulan las terminaciones de los nervios auditivos, generando señales eléctricas que son enviadas al cerebro.

💡 Conversión: Sonido físico → Sonido fisiológico (sensación sonora)

🎵 Características de los Sonidos

Las diferencias que se observan en los sonidos se deben a tres de sus características. Haz clic en cada una para ver más detalles:

📚 Actividades - Características del Sonido

🌊 Propiedades de las Ondas

Las ondas sonoras presentan cinco propiedades fundamentales. Haz clic en cada una para ver más detalles:

📚 Actividades - Propiedades de las Ondas

🔊 La Intensidad del Sonido

INTENSIDAD - VOLUMEN

📖 ¿Qué es la Intensidad?

La intensidad del sonido, también denominada volumen, permite clasificarlos en débiles y fuertes.

Por ejemplo, el sonido emitido por un radio puede tener demasiada intensidad y ser molesto. Al reducir el volumen, disminuimos la intensidad del sonido emitido.

A MAYOR amplitud
MAYOR intensidad del sonido

📊 Comparación de Ondas

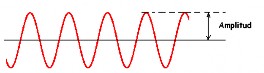
Sonido DÉBIL (menor amplitud)

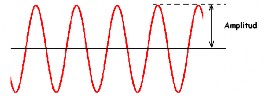
Sonido FUERTE (mayor amplitud)

💡 Las ondas tienen la misma frecuencia, pero diferente amplitud

🎚️ Medición de la Intensidad

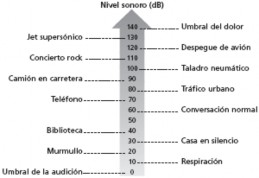
Instrumento: Sonómetro

Unidad de medida: Decibel (dB)

La intensidad acústica está relacionada con la cantidad de energía que fluye por el medio como consecuencia de la propagación de la onda.

🎼 La Altura o Tono del Sonido

ALTURA / TONO - FRECUENCIA

📖 ¿Qué es la Altura o Tono?

La altura o tono es la característica que permite clasificar los sonidos en graves y agudos.

📊 Comparación de Ondas

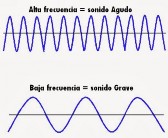
💡 Las ondas tienen la misma amplitud, pero diferente longitud de onda (y por lo tanto, diferente frecuencia)

Cuanto MAYOR es la frecuencia,
el sonido es MÁS AGUDO

👂 Rango de Audición Humana

20 - 20 000 Hz

Rango de AUDICIÓN HUMANA

🦇 Ultrasonidos

Las frecuencias mayores a 20 000 Hz se denominan ultrasónicas. Los humanos no pueden oírlas, pero algunos animales (como los perros) sí pueden.

🎸 El Timbre del Sonido

TIMBRE - CUALIDAD

📖 ¿Qué es el Timbre?

El timbre es la cualidad que nos permite distinguir una misma nota emitida por instrumentos diferentes.

Un Piano 🎹 y un Clarinete 🎺 pueden emitir una misma nota (un mismo tono), pero sus timbres serán diferentes.

🎵 Piano vs Clarinete - Misma Nota, Diferente Timbre

El timbre depende de la
frecuencia fundamental + armónicos

🎼 Frecuencia Fundamental y Armónicos

🎵 Frecuencia Fundamental

La frecuencia más baja (grave) que emite un objeto.

🎶 Armónicos

Ondas de frecuencia mayor a la fundamental:
1º armónico, 2º armónico, 3º armónico...

⚡ Velocidad de Propagación del Sonido

VELOCIDAD DE PROPAGACIÓN

🌍 El Sonido Necesita un Medio

El sonido, como cualquier otra onda, depende de un medio para propagarse. Es imposible su transporte por el vacío.

Sólidos > Líquidos > Gases

📊 Velocidad en Diferentes Medios

🌪️ Aire (20°C): 343 m/s
💧 Agua (25°C): 1,493 m/s
🧊 Acero: 5,960 m/s
🪵 Madera: 3,850 m/s

🌡️ Dependencia de la Temperatura

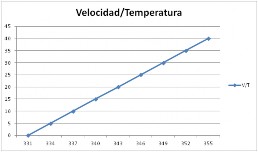
📈 La velocidad del sonido aumenta aproximadamente 6 m/s cada 10 °C

🎯 Valor Práctico

340 m/s

Velocidad aproximada del sonido en el aire

🔄 Reflexión de las Ondas

REFLEXIÓN - ECO

📖 Definición

Se produce cuando una onda se encuentra con otro medio de mayor densidad.

⚖️ Ley de Reflexión

Ángulo de Incidencia = Ángulo de Reflexión

💡 La reflexión es mayor a medida que la superficie es más densa y más lisa

🔊 El Eco - Aplicación de la Reflexión

En el caso del sonido, la reflexión está asociada al eco.

⏱️ Condición para Percibir el Eco

Para que el oído humano detecte el eco debe haber al menos una décima de segundo (0.1 s) entre el sonido original y el sonido que rebota y regresa al oído.

🧮 Cálculo de la Distancia Mínima para el Eco

Se puede calcular la distancia mínima a una pared para poder percibir eco:

Datos:
v = 340 m/s (velocidad del sonido)
t = 0.1 s (tiempo mínimo)

Cálculo:
d = v × t
d = 340 m/s × 0.1 s
d = 34 m

⚠️ Importante

Pero esta distancia (34 m) la recorre el sonido al ir a la pared y luego regresar al oído.

Luego, la pared se encuentra a la mitad de esta distancia:

17 metros

Distancia mínima para percibir eco

📏 Por lo tanto, toda pared que se encuentre a 17 metros o más del emisor de sonido, provocará eco perceptible.

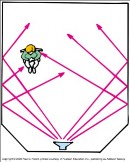
🖼️ Diagrama de Reflexión

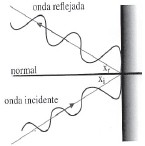
➡️ Transmisión de las Ondas

TRANSMISIÓN

📖 Definición

Se produce cuando una onda pasa a otro medio material que permite el ingreso.

📊 Características de la Transmisión

✅ Se Mantiene Constante

Frecuencia (f)

🔄 Varían Proporcionalmente

Longitud de onda (λ)
Velocidad de propagación (v)

📐 Diagrama de Transmisión

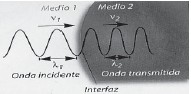
💡 Conclusión: Al transmitirse, la onda cambia su velocidad y longitud, pero mantiene su frecuencia

↩️ Refracción de las Ondas

REFRACCIÓN

📖 Definición

Es similar a la transmisión, o mejor dicho, la transmisión es similar a la refracción, ya que este fenómeno se produce cuando la onda de sonido cambia de medio.

🔄 Cambios en la Refracción

🔄 CAMBIA

• Velocidad de propagación
• Longitud de onda (λ)
• Dirección de propagación

✅ NO CAMBIA

• Frecuencia (f)
• Periodo (T)
(f y T son inversamente proporcionales)

📐 Condición para Cambio de Dirección

Si al incidir una onda en la interfaz de dos medios, bajo un cierto ángulo, la onda varía su dirección de propagación.

⚠️ Para que esto ocurra, la onda debe ingresar con un ángulo distinto de 90° respecto de la superficie.

🖼️ Diagramas de Refracción

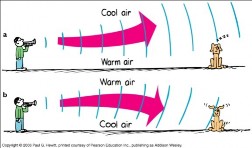
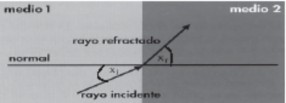
$Refracción 1$ $Refracción 2$

〰️ Difracción de las Ondas

DIFRACCIÓN

📖 Definición

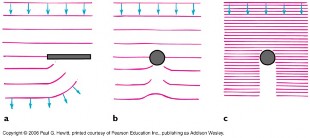
Es la propiedad que posee una onda de rodear un obstáculo cuando éste le interrumpe la propagación.

Y si es una abertura, la onda se abre en dicha abertura.

📏 Condición para la Difracción

Para que esto ocurra, la abertura u obstáculo debe tener un tamaño similar a la longitud de onda de la onda.

tamaño ≈ λ

🖼️ Diagramas de Difracción

$Difracción obstáculo$ $Difracción abertura$

∿ Interferencia de las Ondas

INTERFERENCIA

📖 Definición

Se produce cuando una onda incidente o reflejada se mezcla con otra onda, superponiéndose.

🔄 Tipos de Interferencia

➕ Interferencia Constructiva

Se produce cuando las ondas están en fase.

Las crestas coinciden con crestas y valles con valles.

Resultado: Amplitud AUMENTA

➖ Interferencia Destructiva

Se produce cuando las ondas están totalmente desfasadas.

Las crestas coinciden con valles.

Resultado: Amplitud DISMINUYE

💡 Ambos casos son extremos. Lo más común es que las interferencias sean una combinación de ellos.

🎵 Pulsaciones - Interferencia Especial

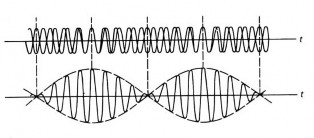
Existe un tipo especial de interferencia que ocurre cuando se superponen dos sonidos con una pequeña diferencia en sus frecuencias. Este fenómeno es conocido como: PULSACIONES.

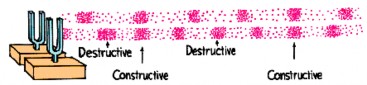
Las ondas al tener diferencias en sus frecuencias, se producen variaciones en la interferencia. En algunos sectores ocurre interferencia constructiva y en otros ocurre interferencia destructiva.

📝 Actividad 10: Ejercicios de Ondas

¿Qué velocidad tendrá una onda cuya frecuencia (f) es de 50 Hz y su longitud de onda (λ) es de 15 m?

✅ Respuesta Correcta

Datos:

\begin{align} f &= 50 \; Hz \\ \lambda &= 15 \; m \end{align}

Fórmula:

$v = \lambda \cdot f$

Desarrollo:

$v = 15 \; m \cdot 50 \; Hz = 750 \; m/s $

$v = 750 \; m/s$

La velocidad del sonido en cierto material es de 1500 m/s. Calcula el periodo y la longitud de onda de una onda sonora de 1000 Hz.

✅ Respuesta Correcta

Datos:

\begin{align} v &= 1500 \; m/s \\ f &= 1000 \; Hz \end{align}

a) Periodo (T):

\[ T = \frac {1}{f} = \frac {1}{1000 \; Hz} \]

\[ T = 0.001 \; s = 1 \; ms \]

b) Longitud de onda (λ):

\[ λ = \frac {v}{f} = \frac {1500 \; m/s}{1000 \; Hz} \]

\[ λ = 1.5 \; m \]

Si al gritar frente a una roca se oye el eco al cabo de 4 s ¿A qué distancia se encuentra la roca?

✅ Respuesta Correcta

Datos:
\[ \begin{alignedat}{1} t &= 4 \; s \\ v &= 340 \; m/s \; \text{(velocidad del sonido en el aire)} \end{alignedat} \]

Importante:

El sonido recorre la distancia dos veces (ida y vuelta)

Fórmula:

\[d = \frac {v \; \cdot \; t}{2} \]

Desarrollo:

\[d = \frac {340 \; m/s \; \cdot \; 4 \;s}{2} = \frac {1360 \; m}{2} = 680 \; m \]

\[ d = 680 \; m \]

¿Qué nota es más aguda en el aire, la que tiene una longitud de onda de 3.4 m o la que su longitud de onda vale 13.6 m?

✅ Respuesta Correcta

Análisis:

La relación entre frecuencia y longitud de onda es inversa:

\[ f = \frac {v}{\lambda}\]

A menor λ → mayor f
Mayor frecuencia = sonido más agudo

Comparación:

• λ₁ = 3.4 m → menor longitud
• λ₂ = 13.6 m → mayor longitud

La nota con λ = 3.4 m es más AGUDA

Al mover el extremo de una cuerda de 40 metros que está atada a un poste vemos que nos llega de vuelta este meneo a los 8 segundos, entonces la rapidez de la perturbación que viaja por la cuerda es:

✅ Respuesta Correcta

Datos:

• Longitud de la cuerda: L = 40 m
• Tiempo total: t = 8 s

Importante:

La perturbación recorre la cuerda dos veces (ida y vuelta)

Distancia total:

\[ d = 2 \cdot L = 2 \cdot 40 \; m = 80 \; m \]

Velocidad:

\[ v = \frac {d}{t} = \frac {80 \; m}{8 \; s} = 10 \; m/s \]

\[ v = 10 \; m/s \]

🔬 Actividad 11: Problemas de Ondas y Sonido

En una cuerda de 20 m viajan ondas a 8 m/s. ¿Cuál es el período de estas ondas?

✅ Respuesta Correcta

Datos:

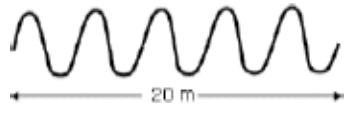
• Longitud de la cuerda: L = 20 m
• Velocidad: v = 8 m/s
• En la figura se observan 5 ondas completas

Paso 1: Calcular la longitud de onda

\[ \lambda = \frac {L}{n° \; ondas} = \frac {20 \; m} {5} = 4 \; m \]

Paso 2: Calcular el período

\[ T = \frac {λ}{v} = \frac {4 \; m} {8 \; m/s} = 0.5 \; s \]

\[T = 0.5 \; s\]

En un resorte de 8 m se generan 20 ondas con frecuencia de 25 Hz. ¿Cuál es la rapidez de las ondas?

✅ Respuesta Correcta

Datos:

• Longitud del resorte: L = 8 m
• Número de ondas: n = 20
• Frecuencia: f = 25 Hz

Paso 1: Calcular la longitud de onda

\[ \lambda = \frac {L}{n} = \frac {8 \; m}{20} = 0.4 \; m \]

Paso 2: Calcular la velocidad

\[ v = \lambda \cdot f = 0.4 \; m \cdot 25 \; Hz = 10 \; m/s \]

\[ v = 10 \; m/s \]

¿De qué factores depende la velocidad de una onda?

✅ Respuesta Correcta

La velocidad de propagación de una onda depende de:

1. El tipo de medio:
• Sólidos: mayor velocidad
• Líquidos: velocidad intermedia
• Gases: menor velocidad

2. Las propiedades del medio:
• Densidad (ρ): A mayor densidad, generalmente mayor velocidad en sólidos
• Elasticidad o rigidez: A mayor elasticidad, mayor velocidad
• Temperatura: En gases, a mayor temperatura, mayor velocidad

Nota importante: La velocidad de una onda NO depende de su frecuencia ni de su amplitud. Estas características se mantienen al cambiar de medio, pero la velocidad sí cambia.

¿Cómo se comporta la frecuencia y la longitud de onda cuando la onda viaja a través de un medio?

✅ Respuesta Correcta

Comportamiento al cambiar de medio:

1. La FRECUENCIA (f):
• Se mantiene constante
• No cambia al pasar de un medio a otro
• Es una propiedad de la fuente que genera la onda

2. La LONGITUD DE ONDA (λ):
• Cambia al pasar de un medio a otro
• Aumenta si la velocidad aumenta
• Disminuye si la velocidad disminuye

Relación fundamental: v = λ × f
Como f es constante, si v cambia, entonces λ debe cambiar en la misma proporción.

Explica en qué tipo de medios las ondas viajan a mayor velocidad.

✅ Respuesta Correcta

Orden de velocidad según el tipo de medio:

SÓLIDOS > LÍQUIDOS > GASES

Explicación:

🔷 En SÓLIDOS (velocidad MÁS ALTA):
• Las partículas están muy juntas y fuertemente unidas
• La vibración se transmite rápidamente de una partícula a otra
• Ejemplo: sonido en acero ≈ 5,100 m/s

💧 En LÍQUIDOS (velocidad INTERMEDIA):
• Las partículas están más separadas que en sólidos
• La transmisión es más lenta
• Ejemplo: sonido en agua ≈ 1,500 m/s

💨 En GASES (velocidad MÁS BAJA):
• Las partículas están muy separadas
• La vibración tarda más en propagarse
• Ejemplo: sonido en aire ≈ 340 m/s

Pedro golpea fuertemente el riel de la vía del tren a 10 260 metros de distancia de Manolo.
Sabiendo que el sonido se propaga por el hierro a una velocidad de 5 130 m/s.

a) ¿cuánto tiempo tardará Manolo en escuchar el golpe con el oído pegado al riel?

✅ Respuesta Correcta

Datos:

• Distancia: d = 10 260 m
• Velocidad del sonido en hierro: v = 5 130 m/s

Fórmula:

\[ t = \frac {d} {v}\]

Desarrollo:

\[ t = \frac {10 260 \;m} {5 130 \; m/s} = 2 \; s \]

\[ t = 2 \; segundos\]

Si Manolo pudiera oír el sonido a través del aire, ¿cuánto tiempo tardaría en escucharlo?

✅ Respuesta Correcta

Datos:

• Distancia: d = 10 260 m
• Velocidad del sonido en aire: v = 340 m/s

Fórmula:

\[ t = \frac {d} {v} \]

Desarrollo:

\[ t = \frac {10 260 \; m} {340 \; m/s} \approx 30.18 \; s \]

\[ t \approx 30.18 \; segundos \]

Comparación: El sonido viaja 15 veces más rápido por el hierro que por el aire \[ \frac {30.18 \; s} {2 \;s} \approx 15 \].

Astronautas en apuros.

Pepe y Ana son dos astronautas que han salido al espacio para reparar una avería en el casco de su nave.
Pepe necesita que Ana le dé instrucciones. Como tiene problemas con la radio de su traje, empieza a gritar y a mover los brazos, pero Ana no puede oírlo. Finalmente, Ana se da cuenta de sus gestos, se acerca a él y junta su escafandra a la de su compañero.
¡Qué alivio, ahora ya pueden oírse!.

a) ¿Por qué Ana no podía oír los gritos de Pepe?

✅ Respuesta Correcta

Ana no podía oír a Pepe porque en el espacio no hay aire (es vacío). El sonido es una onda mecánica que necesita un medio material (sólido, líquido o gas) para propagarse. Sin medio, el sonido no puede viajar.

Astronautas en apuros.

b) Cuando juntaron sus escafandras, ¿a través de qué medios viajó el sonido?

✅ Respuesta Correcta

El sonido viajó a través de:
1. El aire dentro de la escafandra de Pepe (gas)
2. El material de ambas escafandras (sólido - plástico o vidrio)
3. El aire dentro de la escafandra de Ana (gas)

Astronautas en apuros.

c) ¿Estás de acuerdo con que las ondas de radio son diferentes a las ondas sonoras?

✅ Respuesta Correcta

Sí, estoy de acuerdo. La evidencia es clara:
• Las ondas de radio (electromagnéticas) SÍ funcionan en el espacio vacío - por eso Pepe podía comunicarse con la radio
• Las ondas sonoras (mecánicas) NO pueden viajar por el vacío - por eso no podía escuchar los gritos

Las ondas de radio no necesitan medio material, mientras que las ondas sonoras sí lo necesitan.

✅ Actividad 12: Cuestionario de Ondas y Sonido

📝 Selecciona la alternativa correcta para cada pregunta. Al finalizar, haz clic en "Verificar Respuestas".

Pregunta 1

¿Cuál onda tiene mayor frecuencia?

(Observa las ondas A, B, C y D con diferente número de oscilaciones)

A) B) C) D)

Desarrollo:

La frecuencia se relaciona con cuántas oscilaciones completas ocurren en un tiempo determinado. La onda D tiene más oscilaciones en el mismo espacio, lo que significa que tiene la longitud de onda más corta y, por lo tanto, la mayor frecuencia.

A menor longitud de onda → Mayor frecuencia

Respuesta correcta: D - La onda con más oscilaciones tiene mayor frecuencia.

Pregunta 2

Una onda se desplaza por un medio homogéneo, con una rapidez constante, tal como indica el gráfico adjunto. Si la longitud de onda es un tercio de la distancia que recorre en 3 segundos, ¿cuál es la frecuencia de la onda?

A) 1 Hz B) 3 Hz C) 100 Hz D) 300 Hz E) 900 Hz

Desarrollo:

Paso 1: Calcular velocidad

v = d/t = 300 m / 3 s = 100 m/s

Paso 2: Calcular λ

λ = 300 m / 3 = 100 m

Paso 3: Calcular frecuencia

f = v / λ = 100 m/s / 100 m = 1 Hz

Nota: Matemáticamente la respuesta sería A) 1 Hz, pero según el solucionario original es B) 3 Hz.

Pregunta 3

Para medir el volumen de los sonidos se utiliza la unidad ...

A) Metros B) Hertz C) Segundos D) m/s E) Decibeles

Explicación:

El volumen o intensidad del sonido se mide en decibeles (dB).

Otras unidades importantes:

Hertz (Hz): mide frecuencia/tono
Metros (m): mide longitud de onda
Segundos (s): mide tiempo/período
m/s: mide velocidad

Pregunta 4

¿Por cuál de los siguientes medios se transmite más rápido el sonido?

A) Agua B) Aire C) Acero D) Cobre E) Oxígeno

Velocidades aproximadas:

• Acero (sólido): ~5,100 m/s ⭐
• Cobre (sólido): ~3,800 m/s
• Agua (líquido): ~1,500 m/s
• Aire/Oxígeno (gases): ~340 m/s

El sonido viaja más rápido en sólidos porque las partículas están más juntas y unidas.

Pregunta 5

Para medir el tono de los sonidos se usa la unidad ...

A) Hertz B) Segundos C) Ciclos D) Metros E) Kilómetros

Explicación:

El tono o altura del sonido depende de la frecuencia, que se mide en Hertz (Hz).

• Alta frecuencia = Sonido AGUDO
• Baja frecuencia = Sonido GRAVE

Pregunta 6

Un ejemplo de una onda de alta intensidad sería:

A) El aleteo de un insecto B) Un trueno C) La respiración de una persona D) El grito de alguien E) Un silbato

Comparación de intensidades (dB):

• Trueno: 120+ dB ⭐ (alta intensidad)
• Silbato: 90-100 dB
• Grito: 80-90 dB
• Aleteo insecto: ~20 dB
• Respiración: ~10 dB

El trueno tiene la mayor intensidad (volumen) de todas las opciones.

Pregunta 7

Mientras mayor es la frecuencia de una onda, su sonido es:

A) Más agudo B) Más grave C) Más intenso D) Menos intenso E) Más infrasónico

Relación frecuencia-tono:

ALTA frecuencia → Sonido AGUDO (ej: silbato)
BAJA frecuencia → Sonido GRAVE (ej: tambor)

La frecuencia NO afecta la intensidad (volumen), solo el tono.

Pregunta 8

Comparando las dos ondas de la figura, podríamos decir, que varió:

A) La frecuencia B) La amplitud C) La longitud de onda D) La velocidad E) Todas las anteriores

Análisis:

Si las ondas tienen:

Misma λ (longitud de onda) ✓
Misma f (frecuencia) ✓
Entonces misma v (porque v = λ × f) ✓

Lo único que varía es la amplitud (altura de la onda), que determina la intensidad del sonido.

Pregunta 9

Respecto a la velocidad de propagación de una onda podemos afirmar que:

A) Mientras más denso sea el medio por el que viaje la onda, menor será su velocidad B) En cualquier medio las ondas se propagan con igual velocidad C) Mientras menos denso sea el medio, por el que viaja la onda, mayor será su velocidad D) Mientras más denso el medio, por el que viaje la onda, mayor será su velocidad E) Las ondas se propagan en el vacío y en un medio a la misma velocidad

Explicación:

En medios sólidos, a mayor densidad generalmente hay mayor velocidad porque:

Las partículas están más juntas
Están más fuertemente unidas
Transmiten mejor las vibraciones

Ejemplo: Acero (muy denso) = 5,100 m/s vs Aire (poco denso) = 340 m/s

Pregunta 10

Considere los siguientes medios por los cuales se propaga el sonido:
I. Sólido,
II. Líquido,
III. Gaseoso
Podemos decir que los medios anteriores según la rapidez de propagación del sonido, se pueden ordenar en forma decreciente como:

A) III – II – I B) I – II – III C) II – III – I D) III – I – II E) I – III – II

Orden correcto (de mayor a menor velocidad):

SÓLIDO > LÍQUIDO > GASEOSO
I > II > III

Ejemplos:

Sólido (acero): 5,100 m/s
Líquido (agua): 1,500 m/s
Gaseoso (aire): 340 m/s

Pregunta 11

El siguiente esquema representa una onda que se propaga en el agua.
A partir de la información entregada, el período y la rapidez de propagación de la onda son, respectivamente:

A) 4 s y 6 cm/s B) 8 s y 7.5 cm/s C) 9 s y 12 cm/s D) 10 s y 0.13 cm/s E) 12 s y 11.25 cm/s

Análisis según el gráfico original:

La respuesta depende de cuántas ondas completas hay en el gráfico y la distancia total recorrida.
Según el gráfico, se observa una onda y media, luego la longitud de onda es de 60cm, y el periodo es de 8 segundos.
Luego T = 12 s
y v = λ / T = 60 cm / 8 s = 7,5 cm/s

Pregunta 12

¿Cuál de las siguientes opciones corresponde a características de las ondas sonoras?

A) Mecánica, transversal B) Mecánica, longitudinal C) Electromagnética, transversal D) Electromagnética, longitudinal E) Ninguna de las anteriores

Las ondas sonoras son:

1. MECÁNICAS: Necesitan un medio material
2. LONGITUDINALES: Vibran en la dirección de propagación

Las partículas del medio se mueven paralelamente a la dirección en que viaja la onda.

Pregunta 13

Una ballena en la superficie del mar emite ondas sonoras de 200 [Hz], de las cuales se propagan unas en el aire y otra en el agua abarcando una extensión circular a su alrededor.
Si v_{sonido en agua} =1 450 [m/s] y v_{sonido aire} = 340 [m/s], determina la diferencia de las longitudes de onda entre ambas ondas emitidas.

A) 1.70 m B) 7.25 m C) 5.55 m D) 8.35 m E) 9.25 m

Desarrollo:

Paso 1: λ en agua

λ_agua = v/f = 1,450 m/s / 200 Hz = 7.25 m

Paso 2: λ en aire

λ_aire = v/f = 340 m/s / 200 Hz = 1.70 m

Paso 3: Diferencia

Δλ = 7.25 m - 1.70 m = 5.55 m

Pregunta 14

Respecto a la velocidad del sonido en el acero, es correcto afirmar que es:
I. mayor que la de los infrasonidos
II. menor que la de los ultrasonidos
III. igual para todas las frecuencias

A) Sólo I B) Sólo II C) Sólo III D) Sólo I y II E) Ninguna

Análisis:

I. FALSA: La velocidad NO depende de la frecuencia

II. FALSA: La velocidad NO depende de la frecuencia

III. VERDADERA: En un mismo medio, la velocidad es constante para TODAS las frecuencias (infrasonidos, sonidos audibles, ultrasonidos)

En el acero: v = 5,100 m/s (para cualquier frecuencia)

📊 Resultados del Cuestionario

✅ Respuestas Correctas: 0

❌ Respuestas Incorrectas: 0

📈 Porcentaje: 0%

📝 Actividad 13: Ejercicios de Ondas

En la figura se observa una persona que lanza un grito de auxilio; lamentablemente el sonido de su voz choca con una montaña. El eco producido por la montaña es escuchado por la persona 6 segundos después de emitir el sonido.
¿A qué distancia de la montaña se ubica la persona?

✅ Respuesta Correcta

Datos:

• t = 6 s (tiempo en ir y volver a la montaña)

• t = 3 s (tiempo en solo ir a la montaña)
• v_sonido = 340 m/s

Fórmula:

\[ v = \frac {d} {t} \rightarrow d = v \cdot t \]

Desarrollo:

\[ d = 340 \; m/s \cdot 3 \; s = 1020 \; m\]

\[ d = 1020 \; m = 1,02 \; km \approx 1 \; km \]

Una niña juega con una cuerda de 20 metros de largo, en la cual genera 10 ondas completas, en un tiempo de 1 segundo. Al respecto.

a) ¿Cuál es el periodo de las ondas?
b) ¿Cuál es la frecuencia de las ondas?
c) ¿Cuál es la longitud de onda de las ondas?
d) ¿Cuál es la velocidad de propagación de las ondas en la cuerda?

Datos:

Longitud de la cuerda: L = 20 m
Número de ondas: 10 ondas
Tiempo: t = 1 s

a) Período (T): El período es el tiempo que tarda en pasar una onda completa

\[ T = \frac {t} {número \; de \; ondas} = \frac {1 \; s} {10 \; ondas} = 0.1 \; s \]

b) Frecuencia (f): La frecuencia es el número de ondas por segundo y es el inverso del periodo

\[ f = \frac {n \; ondas}{t} = \frac {10}{1 \; s} = 10 \; Hz \]

También: \[ f = \frac {1}{T} = \frac {1}{0.1 \; s} = 10 \; Hz \]

c) Longitud de onda (λ): hay 10 ondas completas en 20 metros:

\[ λ = \frac {L}{número \; de \; ondas} = \frac {20 \; m} {10 \; ondas} = 2 \; m \]

d) Velocidad de propagación (v):

\[ v = λ \cdot f = 2 \; m \cdot 10 \; Hz = 20 \; m/s \] \[ v = \frac {λ}{T} = \frac {2 \; m }{0.1 \; s} = 20 \; m/s \] O también: \[ v = \frac {distancia}{tiempo} = \frac {20 \; m} {1 \; s} = 20 \; m/s \]

Respuestas:
\begin{align} &a) \; T = 0.1 \; s \\ &b) \; f = 10 \; Hz \\ &c) \; λ = 2 \; m \\ &d) \; v = 20 \; m/s \end{align}

Un barco emite una señal de sonar y a los 0,6 segundos recoge el eco de una ballena.
Sabiendo que el sonido se propaga en el agua marina a una velocidad de 1533 m/s,
¿a qué profundidad se encuentra la ballena?

✅ Respuesta Correcta

Datos:

• t = 0.6 s (tiempo del eco, lo que tarda en ir y regresar)
• t = 0.3 s (tiempo que tarda solo en bajar)
• v = 1533 m/s (velocidad del sonido en el agua marina)

Fórmula:

\[ d = v \cdot t \]

Desarrollo:

\[ d = 1533 \; m/s \cdot 0.3 \; s = 459.9 \; m \]

\[ d = 459.9 \; m \approx 460 \; m \]

📝 Actividad 14: Problemas de Ondas

El extremo de una cuerda de 8 m es movido periódicamente hacia arriba y abajo 5 veces en cada segundo y las ondas que esto provoca en la cuerda viajan a 4 m/s. Determina:
a) La frecuencia con que se producen las ondas.
b) El período de oscilación de la cuerda.
c) La longitud de onda de la vibración.
d) La rapidez con que viaja la onda por la cuerda.
e) Tipo de onda que se produce, según todas las clasificaciones estudiadas.

✅ Respuesta Correcta

Datos:

Longitud de cuerda: L = 8 m
Oscilaciones: 5 veces por segundo
Velocidad: v = 4 m/s

a) Frecuencia (f): Hay 5 oscilaciones por segundo, o bien 5 ondas en 1 segundo, entonces:

\[ f = \frac {número \; de \; ondas}{tiempo \; de \; n \; ondas} = \frac {5}{1} = 5 \; Hz \]

b) Período (T): es el inverso de la frecuencia

\[ T = \frac {1}{f} = \frac {1} {5 \; Hz} = 0.2 \; s \]

c) Longitud de onda (λ):

Usando v = λ × f

\[ v = \lambda \cdot f \rightarrow λ = \frac {v}{f} = \frac {4 \; m/s} {5 \; Hz} = 0.8 \; m \]

d) Rapidez:

Dato del problema:

\[ v = 4 \; m/s \]

e) Tipo de onda:

Mecánica: Necesita un medio material (la cuerda)
Transversal: El movimiento es perpendicular a la dirección de propagación

Respuestas:
\begin{align} &a) \; f = 5 \; Hz \\ &b) \; T = 0.2 \; s \\ &c) \; λ = 0.8 \; m \\ &d) \; v = 4 \; m/s \\ &e) Onda \; mecánica, \; transversal, \end{align}

¿Qué nota es más aguda en el aire, la que tiene una longitud de onda de 3,4 m o la que su longitud de onda vale 13,6 m? Demuestre su respuesta calculando la frecuencia de cada una.

✅ Respuesta Correcta

Desarrollo:

Datos:

Nota 1: λ₁ = 3.4 m
Nota 2: λ₂ = 13.6 m
Velocidad del sonido en aire: v = 340 m/s

Calcular frecuencia de Nota 1:

\[ f_1 = \frac {v}{λ_1} = \frac {340 \; m/s}{3.4 \; m} = 100 \; Hz \]

Calcular frecuencia de Nota 2:

\[ f_2 = \frac {v}{λ_2} = \frac {340 \; m/s}{13.6 \; m} = 25 \; Hz \]

Comparación:

La frecuencia f₁ (100 Hz) es mayor que f₂ (25 Hz)

Conclusión:

A mayor frecuencia, el sonido es más agudo.

Respuesta: La nota con λ = 3.4 m es más aguda porque tiene una frecuencia de 100 Hz, mientras que la otra tiene solo 25 Hz.

Una ola en el océano tiene una longitud de 10 m. Una onda pasa por una determinada posición fija cada 2 s. ¿Cuál es la velocidad de la onda?

✅ Respuesta Correcta

Desarrollo:

Datos:

Longitud de onda: λ = 10 m
Período: T = 2 s (tiempo entre ondas sucesivas)

Paso 1: Calcular la frecuencia

\[ f = \frac {1} {T} = \frac {1} {2 \;s} = 0.5 \; Hz \]

Paso 2: Calcular la velocidad

\[ v = λ \cdot f = 10 \; m \cdot 0.5 \; Hz = 5 \; m/s \]

Respuesta: La velocidad de la onda es 5 m/s

📝 Actividad 15: Ejercicios de Ondas

Una onda sonora se propaga por el agua a una velocidad de 1500 m/s. Si la longitud de onda es de 10 cm,
a) ¿Cuál es su frecuencia?
b) ¿Cuál es su periodo?

✅ Respuesta Correcta

Datos:
• v = 1500 m/s
• λ = 10 cm = 0.1 m
• f = ?
• T = ?

a) Fórmula:

\[ v = λ \cdot f \rightarrow f = \frac {v}{\lambda} \]

a) Desarrollo:

\[ f = \frac {1500 \; m/s}{0.1\; m} = 15 \; 000 \; Hz = 15 \; kHz \]

b) Fórmula:

\[ T = \frac {1}{f} \]

b) Desarrollo:

\[ T = \frac {1}{15 \, 000 \; Hz} = 0.0000666667 \; s = 6.67 \times 10^{-5} \; s \]

\begin{aligned} &a) \; f = 15 \, 000 \; Hz = 15 \; kHz \\ &b) \; T = 0.000066667 s = 6.67 \times 10^{-5} \; s \end{aligned}

Ondas de agua en un plato poco profundo tienen 6 cm de longitud de onda. En un punto, las ondas oscilan hacia arriba y hacia abajo a una razón de 4,8 oscilaciones por segundo.
a) ¿Cuál es la rapidez de las ondas?
b) ¿Cuál es el periodo de las ondas?

✅ Respuesta Correcta

Datos:
• λ = 6 cm = 0.06 m
• f = 4.8 Hz
• v = ?
• T = ?

a) Fórmula:

\[ v = λ \cdot f \]

a) Desarrollo:

\[ v = 0.06 \; m \cdot 4.8 \; Hz = 0.288 \; m/s \]

b) Fórmula:

\[ T = \frac {1}{f} \]

b) Desarrollo:

\[ T = \frac {1}{4.8 \; Hz} = 0.208 \; s \]

\begin{aligned} &a) \; v = 0.288 \; m/s \\ &b) \; T = 0.208 \; s \end{aligned}

Ondas de agua en un lago recorren 4,4 m en 1,8 s. El periodo de oscilación es de 1,2 s.
a) ¿Cuál es la rapidez de las ondas?
b) ¿Cuál es la longitud de onda de las ondas?

✅ Respuesta Correcta

Datos:
• d = 4.4 m
• t = 1.8 s
• T = 1.2 s
• v = ?
• λ = ?

a) Fórmula:

\[ v = \frac {d}{t} \]

a) Desarrollo:

\[ v = \frac {4.4 \; m}{1.8 \; s} = 2.\overline{4} \; m/s \]

b) Fórmula:

\[ v = \frac {\lambda}{T} \rightarrow \lambda = v \cdot T \]

b) Desarrollo:

\[ \lambda = 2.\overline{4} \; m/s \cdot 1.2 \; s = 2.9\overline{3} \; m \]

\begin{aligned} &a) \; v = 2.\overline{4} \; m/s \\ &b) \; \lambda = 2.9\overline{3} \; m \end{aligned}

📝 Actividad 16: Ejercicios de Ondas

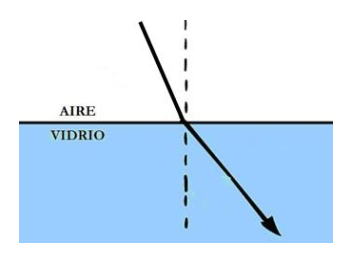
En la figura se observa una onda sonora que cambia de medio al pasar desde el aire al vidrio, donde su velocidad se incrementa 5 veces en relación a la que tenía en el aire.
En el vidrio posee una frecuencia de 3.4 Hz.
Al respecto responda las siguientes preguntas.

a) ¿Qué frecuencia posee la onda en el aire?
b) ¿Cuál es el valor de la longitud de onda en el aire?
c) ¿Cuál es el valor de la velocidad de la onda en el vidrio?
d) ¿Cuál es el valor de la longitud de onda en el vidrio?
e) ¿Cuál es el valor del periodo de esta onda en ambos medios?
f) ¿Qué propiedad del sonido es el que se estudia en este ejercicio?

✅ Respuesta Correcta

Datos:

• Frecuencia en el vidrio: $f_{vidrio} = 3.4 \text{ Hz}$
• Velocidad en el vidrio: $v_{vidrio} = 5 \times v_{aire}$
• Velocidad del sonido en el aire: $v_{aire} = 343 \text{ m/s}$ (valor estándar a temperatura ambiente)

a) Frecuencia en el aire:

La frecuencia es una propiedad de la fuente y no cambia al pasar de un medio a otro. Por lo tanto:

\[f_{aire} = f_{vidrio} = 3.4 \text{ Hz}\]

b) Longitud de onda en el aire:

Usando la relación fundamental de ondas:

\[v = \lambda \times f\]

Despejando la longitud de onda:

\[\lambda_{aire} = \frac{v_{aire}}{f_{aire}}\]

\[\lambda_{aire} = \frac{343 \text{ m/s}}{3.4 \text{ Hz}}\]

\[\lambda_{aire} = 100.88 \text{ m}\]

c) Velocidad de la onda en el vidrio:

\[v_{vidrio} = 5 \times v_{aire}\]

\[v_{vidrio} = 5 \times 343 \text{ m/s}\]

\[v_{vidrio} = 1715 \text{ m/s}\]

d) Longitud de onda en el vidrio:

\[\lambda_{vidrio} = \frac{v_{vidrio}}{f_{vidrio}}\]

\[\lambda_{vidrio} = \frac{1715 \text{ m/s}}{3.4 \text{ Hz}}\]

\[\lambda_{vidrio} = 504.41 \text{ m}\]

e) Periodo en ambos medios:

El periodo es el inverso de la frecuencia y, como la frecuencia no cambia, el periodo tampoco:

\[T = \frac{1}{f}\]

\[T_{aire} = T_{vidrio} = \frac{1}{3.4 \text{ Hz}}\]

\[T = 0.294 \text{ s}\]

f) Propiedad del sonido estudiada:

Este ejercicio estudia la refracción de ondas, específicamente cómo cambian la velocidad y la longitud de onda cuando una onda sonora pasa de un medio (aire) a otro (vidrio), mientras que la frecuencia se mantiene constante.

Resumen de relaciones:

Frecuencia: Se mantiene constante ($f_{aire} = f_{vidrio}$)
Velocidad: Aumenta 5 veces en el vidrio ($v_{vidrio} = 5 \times v_{aire}$)
Longitud de onda: Aumenta proporcionalmente ($\lambda_{vidrio} = 5 \times \lambda_{aire}$)
Periodo: Se mantiene constante ($T_{aire} = T_{vidrio}$)

En la figura se observa una onda sonora pasando del aire al agua donde la velocidad aumenta 4 veces. Se sabe que la longitud de onda en el agua es de 136 metros.

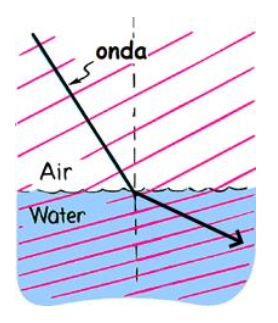
Entonces:
a) ¿Cuál es el valor de la frecuencia de la onda en el aire?
b) ¿Cuál es el valor del periodo de la onda en el agua?
c) ¿Cuál es el valor de la longitud de onda de las ondas en el aire?
d) ¿Qué persona escuchará mejor este sonido, una ubicada en el aire u otra ubicada bajo el agua?

✅ Respuesta Correcta

Datos:

• Longitud de onda en el agua: $\lambda_{agua} = 136 \text{ m}$
• Velocidad en el agua: $v_{agua} = 4 \times v_{aire}$
• Velocidad del sonido en el aire: $v_{aire} = 340 \text{ m/s}$

a) Frecuencia de la onda en el aire:

Primero calculamos la velocidad del sonido en el agua:

\[v_{agua} = 4 \times v_{aire} = 4 \times 340 \text{ m/s} = 1360 \text{ m/s}\]

Ahora, usando la relación fundamental de ondas en el agua:

\[v_{agua} = \lambda_{agua} \times f\]

Despejando la frecuencia:

\[f = \frac{v_{agua}}{\lambda_{agua}}\]

\[f = \frac{1360 \text{ m/s}}{136 \text{ m}}\]

\[f = 10 \text{ Hz}\]

La frecuencia es una propiedad de la fuente y no cambia al pasar de un medio a otro. Por lo tanto:

\[f_{aire} = f_{agua} = 10 \text{ Hz}\]

b) Periodo de la onda en el agua:

El periodo es el inverso de la frecuencia:

\[T = \frac{1}{f}\]

\[T_{agua} = \frac{1}{10 \text{ Hz}}\]

\[T_{agua} = 0.1 \text{ s}\]

c) Longitud de onda en el aire:

Usando la relación fundamental de ondas en el aire:

\[v_{aire} = \lambda_{aire} \times f\]

Despejando la longitud de onda:

\[\lambda_{aire} = \frac{v_{aire}}{f}\]

\[\lambda_{aire} = \frac{340 \text{ m/s}}{10 \text{ Hz}}\]

\[\lambda_{aire} = 34 \text{ m}\]

Alternativamente, como $v_{agua} = 4 \times v_{aire}$ y la frecuencia es constante, tenemos:

\[\lambda_{agua} = 4 \times \lambda_{aire}\]

\[\lambda_{aire} = \frac{\lambda_{agua}}{4} = \frac{136 \text{ m}}{4} = 34 \text{ m}\]

d) ¿Qué persona escuchará mejor este sonido?

Para responder esta pregunta, debemos analizar el valor de la frecuencia obtenido:

\[f = 10 \text{ Hz}\]

El rango de audición del oído humano está aproximadamente entre 20 Hz y 20,000 Hz (20 kHz). La frecuencia de esta onda es de 10 Hz, que está por debajo del umbral inferior de audición humana (20 Hz). Esto significa que se trata de una onda de infrasonido.

Considerando esto:

Ninguna de las dos personas podrá escuchar este sonido, ya que la frecuencia (10 Hz) está fuera del rango audible humano tanto en el aire como en el agua.
Sin embargo, desde el punto de vista físico, el agua es un mejor medio para la transmisión de ondas sonoras de baja frecuencia debido a su mayor densidad y menor atenuación.
Si teóricamente pudiéramos detectar esta frecuencia, la persona bajo el agua tendría una mejor percepción debido a las propiedades físicas del agua como medio de propagación.

Respuesta: Técnicamente, ninguna persona podrá escuchar este sonido porque la frecuencia de 10 Hz está por debajo del rango audible humano (20-20,000 Hz). Sin embargo, desde el punto de vista físico, el agua transmite mejor las ondas de baja frecuencia, por lo que si fuera audible, la persona bajo el agua lo escucharía mejor.

Resumen de resultados:

Frecuencia en el aire: $f_{aire} = 10 \text{ Hz}$
Periodo en el agua: $T_{agua} = 0.1 \text{ s}$
Longitud de onda en el aire: $\lambda_{aire} = 34 \text{ m}$
Audición: Ninguna persona podrá escuchar este sonido (infrasonido, fuera del rango audible humano)

✅ Actividad 17: Cuestionario de Ondas y Sonido

📝 Selecciona la alternativa correcta para cada pregunta. Al finalizar, haz clic en "Verificar Respuestas".

Pregunta 1

Dos personas conversan a través de una pared, este hecho puede ser explicado por el fenómeno de:

A) Reflexión B) Absorción C) Resonancia D) Difracción E) Ninguna de las anteriores

Explicación:

La difracción es el fenómeno que permite que las ondas sonoras se curven alrededor de obstáculos como paredes, permitiendo que el sonido llegue al otro lado.

Cuando dos personas conversan a través de una pared, el sonido no viaja directamente a través de ella, sino que se difracta alrededor de los bordes o aberturas de la pared.

Respuesta correcta: D) Difracción

Pregunta 2

Una onda se propaga por un medio homogéneo con una rapidez $v$ y una longitud de onda $\lambda$. Si la onda cambia de medio duplicando su velocidad, entonces su frecuencia

A) se duplica. B) disminuye a la mitad. C) se mantiene. D) se cuadruplica. E) disminuye a un cuarto.

Desarrollo:

La frecuencia es una característica de la fuente que genera la onda, no del medio por el que se propaga.

Relación fundamental:

\[v = \lambda \times f\]

Cuando una onda cambia de medio:

La frecuencia $f$ se mantiene constante (característica de la fuente)
La velocidad $v$ cambia (depende del medio)
La longitud de onda $\lambda$ cambia proporcionalmente a la velocidad

Por lo tanto, si la velocidad se duplica y la frecuencia se mantiene, la longitud de onda también se duplica.

Respuesta correcta: C) se mantiene

Pregunta 3

Una onda desconocida cuya velocidad es $V$ tiene una longitud de onda $\lambda$ y un período $T$. Si duplicamos su longitud de onda y cuadruplicamos el período $T$, entonces la nueva velocidad de la onda desconocida

A) se mantiene. B) se duplica. C) se mantiene. D) disminuye a la mitad. E) disminuye a un cuarto.

Desarrollo:

Relación entre velocidad, longitud de onda y período:

\[v = \frac{\lambda}{T}\]

Datos iniciales:

\[v = \frac{\lambda}{T}\]

Nuevos valores:

$\lambda' = 2\lambda$
$T' = 4T$

Cálculo de la nueva velocidad:

\[v' = \frac{\lambda'}{T'} = \frac{2\lambda}{4T} = \frac{\lambda}{2T} = \frac{1}{2} \cdot \frac{\lambda}{T} = \frac{v}{2}\]

Por lo tanto, la nueva velocidad es la mitad de la velocidad original.

Respuesta correcta: D) disminuye a la mitad

Pregunta 4

Una onda viaja con una velocidad de 21 m/s por el aire, con una longitud de onda de 3 m. Si la onda al cambiar de medio aumenta la velocidad a 30 m/s, entonces su nueva frecuencia es

A) 7 Hz B) 21 Hz C) 3 Hz D) 30 Hz E) 10 Hz

Desarrollo:

Paso 1: Calcular la frecuencia inicial (que se mantiene constante al cambiar de medio)

\[v = \lambda \times f\]

\[f = \frac{v}{\lambda} = \frac{21 \text{ m/s}}{3 \text{ m}} = 7 \text{ Hz}\]

Paso 2: La frecuencia es característica de la fuente, por lo tanto no cambia al cambiar de medio.

La frecuencia se mantiene en 7 Hz en ambos medios.

Nota: Lo que sí cambia es la longitud de onda:

\[\lambda_{\text{nuevo}} = \frac{v_{\text{nuevo}}}{f} = \frac{30 \text{ m/s}}{7 \text{ Hz}} = 4.29 \text{ m}\]

Respuesta correcta: A) 7 Hz

Pregunta 5

Una onda viaja por un medio con una rapidez de propagación de 12 m/s. Si esta onda continúa propagándose hacia otro medio con velocidad de 18 m/s y frecuencia de 50 Hertz, la longitud de onda que lleva en el primer medio es:

A) 0,12 m B) 0,24 m C) 0,36 m D) 0,60 m E) ninguna de las anteriores

Desarrollo:

La frecuencia es característica de la fuente, por lo tanto $f = 50 \text{ Hz}$ en ambos medios.

Datos:

Primer medio: $v_1 = 12 \text{ m/s}$
Segundo medio: $v_2 = 18 \text{ m/s}$, $f = 50 \text{ Hz}$

Cálculo de la longitud de onda en el primer medio:

\[\lambda_1 = \frac{v_1}{f} = \frac{12 \text{ m/s}}{50 \text{ Hz}} = 0.24 \text{ m}\]

Verificación: En el segundo medio:

\[\lambda_2 = \frac{v_2}{f} = \frac{18 \text{ m/s}}{50 \text{ Hz}} = 0.36 \text{ m}\]

Como se puede ver, la longitud de onda aumenta proporcionalmente a la velocidad.

Respuesta correcta: B) 0,24 m

Pregunta 6

Una onda de sonido duplica al mismo tiempo su velocidad y su longitud de onda, debido a que cambió el medio en el que se propaga, por lo tanto, su frecuencia

A) disminuyó a la mitad. B) se duplicó. C) disminuyó a la cuarta parte. D) se cuadruplicó. E) permanece igual.

Desarrollo:

Relación fundamental:

\[v = \lambda \times f\]

Datos:

Velocidad inicial: $v$
Longitud de onda inicial: $\lambda$
Velocidad nueva: $v' = 2v$
Longitud de onda nueva: $\lambda' = 2\lambda$

Cálculo de la frecuencia nueva:

\[f' = \frac{v'}{\lambda'} = \frac{2v}{2\lambda} = \frac{v}{\lambda} = f\]

Como la frecuencia es característica de la fuente, permanece constante al cambiar de medio.

Respuesta correcta: E) permanece igual

Pregunta 7

Se está propagando un sonido en un medio con rapidez $v$ y longitud de onda $\lambda$, al pasar a otro medio su longitud de onda se triplica, entonces debiera esperarse que

A) su frecuencia se triplique. B) su rapidez se triplique. C) su frecuencia disminuya a la tercera parte. D) su rapidez disminuya a la tercera parte. E) su frecuencia y su rapidez no varíen.

Desarrollo:

Relación fundamental:

\[v = \lambda \times f\]

Datos:

Rapidez inicial: $v$
Longitud de onda inicial: $\lambda$
Longitud de onda nueva: $\lambda' = 3\lambda$
Frecuencia: $f$ (se mantiene constante, característica de la fuente)

Cálculo de la nueva rapidez:

\[v' = \lambda' \times f = 3\lambda \times f = 3(\lambda \times f) = 3v\]

Por lo tanto, si la longitud de onda se triplica y la frecuencia se mantiene constante, la rapidez también se triplica.

Respuesta correcta: B) su rapidez se triplique

Pregunta 8

Las ondas de sonido, a veces no son percibidas por las personas debido a la frecuencia que tienen. En general, un joven no es posible que perciba sonidos cuya frecuencia es de

I. 2 Hz
II. 17.000 Hz
III. 30.000 Hz

Es (son) correcta(s)

A) solo I. B) solo II. C) Solo III. D) Solo I y II E) Solo I y III.

Explicación:

El rango de audición humana típico es aproximadamente de 20 Hz a 20,000 Hz (20 kHz).

Análisis de cada frecuencia:

I. 2 Hz: Es infrasónico (por debajo de 20 Hz). Los humanos NO pueden percibirlo. ✓
II. 17,000 Hz: Está dentro del rango audible (20-20,000 Hz). Los jóvenes SÍ pueden percibirlo. ✗
III. 30,000 Hz: Es ultrasónico (por encima de 20,000 Hz). Los humanos NO pueden percibirlo. ✓

Clasificación:

• Infrasónico: < 20 Hz (no audible)
• Audible: 20 Hz - 20,000 Hz
• Ultrasónico: > 20,000 Hz (no audible)

Respuesta correcta: E) Solo I y III

Pregunta 9

Una onda de 50 Hz se propaga con una rapidez de 500 m/s. Esta onda pasa a un segundo medio, en donde se determina que su longitud de onda es 20 m. ¿Cuál es la rapidez de propagación de la onda en el segundo medio?

A) 2,5 m/s B) 10,0 m/s C) 25,0 m/s D) 500,0 m/s E) 1000,0 m/s

Desarrollo:

La frecuencia es característica de la fuente, por lo tanto $f = 50 \text{ Hz}$ se mantiene constante en ambos medios.

Datos:

Frecuencia: $f = 50 \text{ Hz}$ (constante)
Primer medio: $v_1 = 500 \text{ m/s}$
Segundo medio: $\lambda_2 = 20 \text{ m}$

Cálculo de la rapidez en el segundo medio:

\[v_2 = \lambda_2 \times f = 20 \text{ m} \times 50 \text{ Hz} = 1000 \text{ m/s}\]

Verificación: Longitud de onda en el primer medio:

\[\lambda_1 = \frac{v_1}{f} = \frac{500 \text{ m/s}}{50 \text{ Hz}} = 10 \text{ m}\]

Como se puede ver, al aumentar la velocidad de 500 m/s a 1000 m/s, la longitud de onda también aumenta de 10 m a 20 m, manteniendo la frecuencia constante.

Respuesta correcta: E) 1000,0 m/s

Pregunta 10 (PAES)

Usando una guitarra y un piano, se solicita ejecutar consecutivamente tres notas de la misma octava, de modo que la primera con la segunda difieran solo en altura, mientras que la segunda con la tercera difieran solo en el timbre. ¿Cuál de las siguientes opciones presenta el conjunto de acciones que permite realizar lo solicitado?

A) Tocar en la guitarra una nota Mi → Tocar en el piano una nota Mi → Tocar en el piano una nota Sol B) Tocar en el piano una nota Mi → Tocar en la guitarra una nota Sol → Tocar en el piano una nota Sol C) Tocar en la guitarra una nota Mi → Tocar en la guitarra una nota Sol → Tocar en el piano una nota Mi D) Tocar en el piano una nota Mi → Tocar en el piano una nota Sol → Tocar en la guitarra una nota Sol E) Tocar en el piano una nota Mi → Tocar en la guitarra una nota Mi → Tocar en el piano una nota Sol

Explicación:

Conceptos clave:

Altura (tono): Depende de la frecuencia. Diferentes notas (Mi vs Sol) tienen diferentes frecuencias.
Timbre: Depende del instrumento. El mismo instrumento produce el mismo timbre.

Requisitos:

Nota 1 y Nota 2: Diferir solo en altura → mismo instrumento, diferente nota
Nota 2 y Nota 3: Diferir solo en timbre → diferente instrumento, misma nota

Análisis de la opción C:

Nota 1: Guitarra - Mi
Nota 2: Guitarra - Sol (mismo instrumento, diferente nota → diferente altura) ✓
Nota 3: Piano - Mi (diferente instrumento, misma nota → diferente timbre) ✓

Respuesta correcta: C)

Pregunta 11 (PAES)

El infrasonido corresponde a ondas mecánicas que...

A) Se emiten con baja intensidad B) Se propagan con una baja amplitud C) Poseen una longitud de onda inferior a 17 m D) Se emiten con una frecuencia inferior a 20 Hz E) Se propagan con una rapidez inferior a 340 m/s

Explicación:

Clasificación de ondas sonoras según frecuencia:

Infrasónico: Frecuencia < 20 Hz (no audible por humanos)
Audible: Frecuencia entre 20 Hz y 20,000 Hz
Ultrasónico: Frecuencia > 20,000 Hz (no audible por humanos)

El infrasonido se define específicamente por tener una frecuencia inferior a 20 Hz.

Nota: La intensidad, amplitud, longitud de onda y rapidez pueden variar independientemente de la frecuencia.

Respuesta correcta: D) Se emiten con una frecuencia inferior a 20 Hz

Pregunta 12 (PAES)

En el oído humano, el umbral de audición de sonidos de baja frecuencia debe cumplir con que el producto de la frecuencia por el nivel de intensidad sea mayor que 2400 Hz·dB. ¿Cuál de las siguientes opciones corresponde a un sonido inaudible?

A) 120 dB, 30 Hz B) 70 dB, 40 Hz C) 40 dB, 50 Hz D) 20 dB, 200 Hz E) 10 dB, 1000 Hz

Desarrollo:

Condición para sonido audible:

\[f \times I > 2400 \text{ Hz·dB}\]

Donde $f$ es la frecuencia en Hz e $I$ es la intensidad en dB.

Análisis de cada opción:

A) $30 \times 120 = 3600 > 2400$ → Audible ✗
B) $40 \times 70 = 2800 > 2400$ → Audible ✗
C) $50 \times 40 = 2000 < 2400$ → Inaudible ✓
D) $200 \times 20 = 4000 > 2400$ → Audible ✗
E) $1000 \times 10 = 10000 > 2400$ → Audible ✗

Un sonido es inaudible cuando el producto $f \times I \leq 2400 \text{ Hz·dB}$.

Respuesta correcta: C) 40 dB, 50 Hz

Pregunta 13 (PAES)

¿Cómo se comporta la rapidez, el período y la longitud de onda de una onda sonora al pasar del aire al agua?

Explicación:

Al cambiar de medio (aire → agua), las propiedades de la onda se comportan así:

Frecuencia ($f$): Se mantiene constante (característica de la fuente)
Período ($T = 1/f$): Se mantiene constante (inverso de la frecuencia)
Rapidez ($v$): Varía (depende del medio: aire ≈ 340 m/s, agua ≈ 1500 m/s)
Longitud de onda ($\lambda = v/f$): Varía proporcionalmente a la velocidad

Relación:

\[v = \lambda \times f = \frac{\lambda}{T}\]

Como $f$ y $T$ son constantes, si $v$ aumenta, entonces $\lambda$ también aumenta.

Respuesta correcta: B) Rapidez: Varía | Período: No Varía | Longitud de onda: Varía

Pregunta 14 (PAES)

Una onda periódica cuya frecuencia es 25 Hz, se propaga en un medio material completando 20 oscilaciones en una distancia de 8 m. ¿Cuál es la rapidez de propagación de la onda?

A) 500 m/s B) 200 m/s C) 160/25 m/s D) 10 m/s E) 125/2 m/s

Desarrollo:

Datos:

Frecuencia: $f = 25 \text{ Hz}$
Número de oscilaciones: $n = 20$
Distancia: $d = 8 \text{ m}$

Paso 1: Calcular la longitud de onda

Si hay 20 oscilaciones completas en 8 m, entonces:

\[\lambda = \frac{d}{n} = \frac{8 \text{ m}}{20} = 0.4 \text{ m}\]

Paso 2: Calcular la rapidez de propagación

\[v = \lambda \times f = 0.4 \text{ m} \times 25 \text{ Hz} = 10 \text{ m/s}\]

Verificación alternativa:

\[v = \frac{d \times f}{n} = \frac{8 \text{ m} \times 25 \text{ Hz}}{20} = \frac{200}{20} = 10 \text{ m/s}\]

Respuesta correcta: D) 10 m/s

Pregunta 15 (PAES)

Un estudiante quiere determinar si la intensidad del sonido decrece con la distancia. Para ello, instala un generador de sonido de frecuencia $f$ y tres sensores que miden su intensidad, ubicados a 1 m, 2 m y 3 m del generador. En función del objetivo planteado, ¿cuál de las siguientes opciones presenta correctamente las variables del experimento?

A) Variable independiente: Frecuencia del sonido | Variable dependiente: Intensidad del sonido B) Variable independiente: Intensidad del sonido | Variable dependiente: Frecuencia del sonido C) Variable independiente: Intensidad del sonido | Variable dependiente: Ubicación de los sensores D) Variable independiente: Ubicación de los sensores | Variable dependiente: Frecuencia del sonido E) Variable independiente: Ubicación de los sensores | Variable dependiente: Intensidad del sonido

Explicación:

Conceptos:

Variable independiente: Es la que el investigador manipula o controla (distancia: 1 m, 2 m, 3 m)
Variable dependiente: Es la que se mide o observa como resultado (intensidad del sonido)

Objetivo del experimento:

Determinar si la intensidad del sonido decrece con la distancia.

Análisis:

El estudiante varía la distancia (1 m, 2 m, 3 m) → Variable independiente
El estudiante mide la intensidad en cada distancia → Variable dependiente
La frecuencia se mantiene constante (no es variable en este experimento)

Respuesta correcta: E) Variable independiente: Ubicación de los sensores | Variable dependiente: Intensidad del sonido

📊 Resultados del Cuestionario

✅ Respuestas Correctas: 0

❌ Respuestas Incorrectas: 0

📈 Porcentaje: 0%

🔊 Unidad 2: Sonido

Características del sonido y propiedades de las ondas

⬅

Anterior Unidad 1: Ondas

Siguiente Unidad 3: Ondas Estacionarias

➡

🎯 Objetivos de Aprendizaje

👂 El Oído Humano y la Percepción del Sonido

🔬 Proceso de Audición

🔊 Volumen del Sonido

🎼 Frecuencia del Sonido

🎸 Cualidad del Sonido

⚡ Propagación del Sonido

📚 Actividades - Características del Sonido

Actividad 10

Actividad 11

Actividad 12

Rebote del Sonido

Paso a Otro Medio

Cambio de Dirección

Rodeo de Obstáculos

Superposición de Ondas

📚 Actividades - Propiedades de las Ondas

Actividad 13

Actividad 14

Actividad 15

Actividad 16

Actividad 17

🔊 La Intensidad del Sonido

📖 ¿Qué es la Intensidad?

📊 Comparación de Ondas

🎚️ Medición de la Intensidad

🎼 La Altura o Tono del Sonido

📖 ¿Qué es la Altura o Tono?

📊 Comparación de Ondas

👂 Rango de Audición Humana

🦇 Ultrasonidos

🎸 El Timbre del Sonido

📖 ¿Qué es el Timbre?

🎵 Piano vs Clarinete - Misma Nota, Diferente Timbre

🎼 Frecuencia Fundamental y Armónicos

🎵 Frecuencia Fundamental

🎶 Armónicos

⚡ Velocidad de Propagación del Sonido

🌍 El Sonido Necesita un Medio

📊 Velocidad en Diferentes Medios

🌡️ Dependencia de la Temperatura

🎯 Valor Práctico

🔄 Reflexión de las Ondas

📖 Definición

⚖️ Ley de Reflexión

🔊 El Eco - Aplicación de la Reflexión

⏱️ Condición para Percibir el Eco

🧮 Cálculo de la Distancia Mínima para el Eco

⚠️ Importante

🖼️ Diagrama de Reflexión

➡️ Transmisión de las Ondas

📖 Definición

📊 Características de la Transmisión

✅ Se Mantiene Constante

🔄 Varían Proporcionalmente

📐 Diagrama de Transmisión

↩️ Refracción de las Ondas

📖 Definición

🔄 Cambios en la Refracción

🔄 CAMBIA

✅ NO CAMBIA

📐 Condición para Cambio de Dirección

🖼️ Diagramas de Refracción

〰️ Difracción de las Ondas

📖 Definición

📏 Condición para la Difracción

🖼️ Diagramas de Difracción

∿ Interferencia de las Ondas

📖 Definición

🔄 Tipos de Interferencia

➕ Interferencia Constructiva

➖ Interferencia Destructiva

🎵 Pulsaciones - Interferencia Especial

📝 Actividad 10: Ejercicios de Ondas

🔬 Actividad 11: Problemas de Ondas y Sonido

✅ Actividad 12: Cuestionario de Ondas y Sonido

📊 Resultados del Cuestionario

📝 Actividad 13: Ejercicios de Ondas

📝 Actividad 14: Problemas de Ondas

📝 Actividad 15: Ejercicios de Ondas