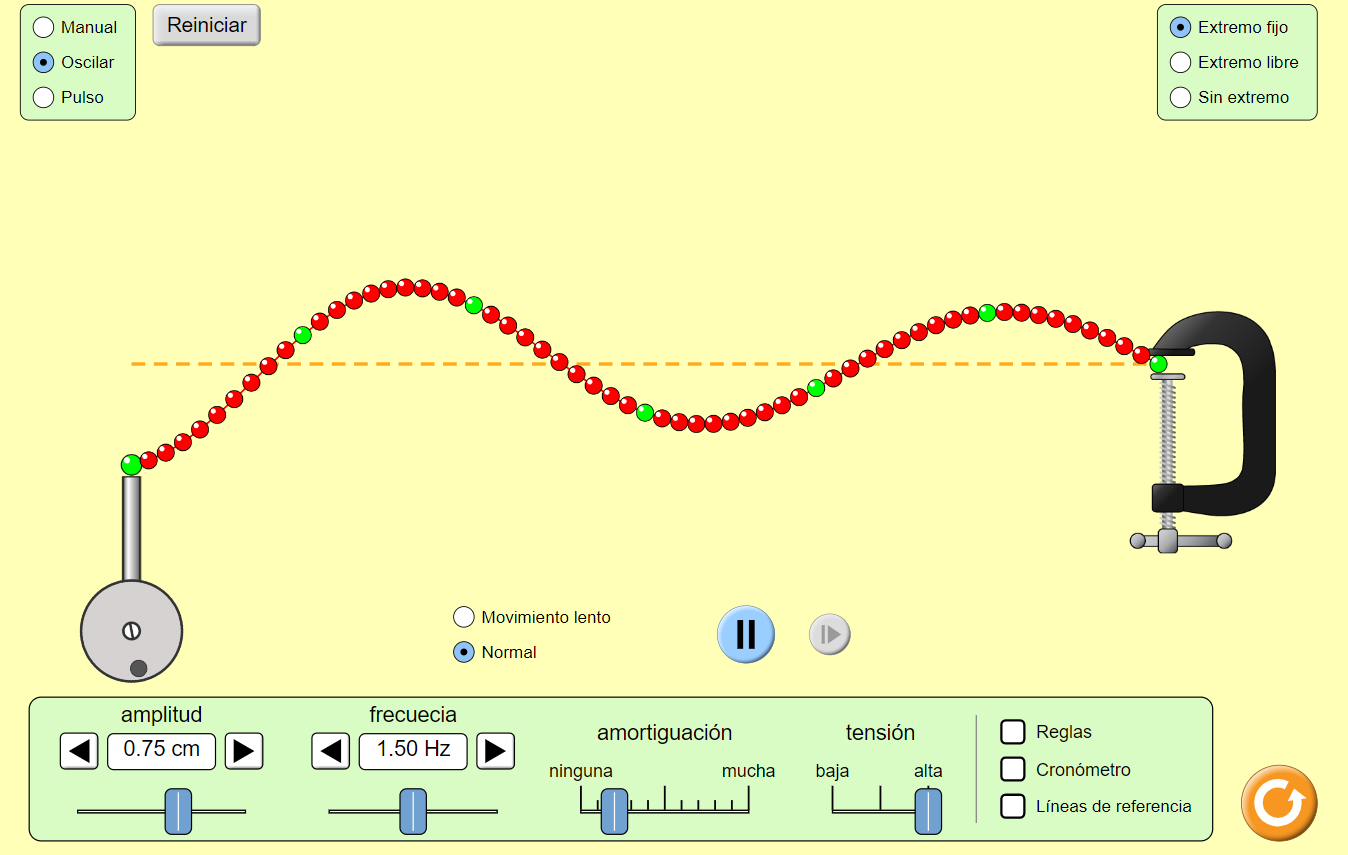
⏱️ Elementos No Visibles de una Onda
Otros elementos de una onda que no se pueden ver, pero que se pueden medir son:
👆 Haz clic en cada elemento para ver sus detalles:
⏰ PERÍODO (T)
📖 Definición
El período es el tiempo que transcurre para que una posición determinada de una onda (podemos identificarla con un punto del medio) recorra una longitud de onda completa.
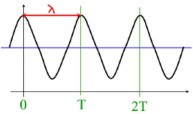
El período (T) es el tiempo para completar un ciclo completo
🔍 Características del Período
- Unidad de medida: Se mide en unidades de tiempo (segundos, s)
- Notación: Se identifica con la letra T
- Concepto clave: Tiempo para completar un ciclo u oscilación
- Relación con frecuencia: T = 1 / f
💡 Concepto Importante: Ciclo u Oscilación
Cuando un punto completa el recorrido correspondiente a un período se dice que ha descrito:
- Un ciclo
- Una oscilación
- Una revolución (cuando el movimiento ondulatorio se relaciona con un movimiento circunferencial)
📐 Fórmula del Período
T = 1 / f
El período es el inverso de la frecuencia
🔢 Ejemplos
Si f = 2 Hz:
T = 1 / 2 = 0.5 segundos
Cada ciclo dura medio segundo
Si f = 100 Hz:
T = 1 / 100 = 0.01 segundos
Cada ciclo dura una centésima de segundo
📊 FRECUENCIA (f)
📖 Definición
El concepto de frecuencia está asociado a un número que precisa la cantidad de ciclos o revoluciones que se producen en la unidad de tiempo, que generalmente es el segundo, aunque en ocasiones es el minuto.
🔍 Características de la Frecuencia
- Unidad de medida: Cuando el período se expresa en segundos (s), la frecuencia se expresa en s-1 (segundo elevado a menos uno)
- Nombre de la unidad: Hertz (Hz)
- Notación: Se designa con la letra f
- Relación con período: La frecuencia es el inverso multiplicativo del período
📐 Fórmula: Relación Período-Frecuencia
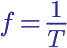
f = 1 / T
La frecuencia es el inverso del período
💡 Significado de Hertz (Hz)
1 Hz significa 1 oscilación (ciclo) por segundo
Por lo tanto, cuando decimos que una onda tiene una frecuencia de 50 Hz, significa que completa 50 oscilaciones cada segundo.
🔢 Ejemplos Prácticos
2 Hz
= 2 oscilaciones en 1 segundo
T = 1/2 = 0.5 s
50 Hz
= 50 oscilaciones en 1 segundo
T = 1/50 = 0.02 s
1200 Hz
= 1200 oscilaciones en 1 segundo
T = 1/1200 ≈ 0.00083 s
🎵 Ejemplos en la Vida Real
- Nota La (440 Hz): Vibra 440 veces por segundo
- Corriente eléctrica (50-60 Hz): La corriente alterna oscila 50 o 60 veces por segundo según el país
- Radio FM (88-108 MHz): Millones de oscilaciones por segundo
- Procesador (3 GHz): 3 mil millones de ciclos por segundo
🚀 VELOCIDAD DE PROPAGACIÓN (v)
📖 Definición
La velocidad de propagación de la onda es un concepto que representa la rapidez de cambio de posición de un punto (o región de un medio) a través del tiempo.
Relaciona los conceptos de longitud de onda y período.
🔍 Características de la Velocidad
- Notación: Se denota con la letra v
- Unidad: metros por segundo (m/s)
- Concepto: Rapidez con que se propaga la onda
- Relación: Conecta longitud de onda, período y frecuencia
- Depende del medio: Varía según las propiedades del medio de propagación
📐 TRES FÓRMULAS DE LA VELOCIDAD
1️⃣ Velocidad con Longitud de Onda y Período
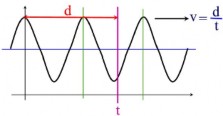
v = λ / T
Velocidad = Longitud de onda / Período
2️⃣ Velocidad con Longitud de Onda y Frecuencia
Si consideramos que f = 1 / T, entonces:
v = λ · f
Velocidad = Longitud de onda × Frecuencia
⭐ Esta es la fórmula más utilizada para calcular la velocidad de propagación
3️⃣ Velocidad como Distancia / Tiempo
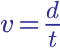
v = d / t
Velocidad = Distancia recorrida / Tiempo transcurrido
💡 Esta es la fórmula general de velocidad en física
🔢 Ejemplo de Cálculo
Datos:
- Longitud de onda (λ) = 2 metros
- Frecuencia (f) = 5 Hz
Calcular la velocidad:
v = λ · f
v = 2 m × 5 Hz
v = 10 m/s
La onda se propaga a 10 metros por segundo
🌊 Velocidades de Ondas Comunes
🎮 Simulación Interactiva PhET
Experimenta con ondas en una cuerda y observa cómo cambian el período, la frecuencia y otros elementos:
📋 Resumen de Fórmulas
| Magnitud | Símbolo | Fórmula Principal | Unidad |
|---|---|---|---|
| Período | T | T = 1 / f | segundos (s) |
| Frecuencia | f | f = 1 / T | Hertz (Hz) = s-1 |
| Velocidad | v | v = λ · f = λ / T | metros/segundo (m/s) |
📚 Actividades de Práctica
Pon en práctica lo aprendido con las siguientes actividades:
📝 Actividad 2
Dibujo y análisis de ondas
📊 Actividad 3
Cálculos con fórmulas
🎯 Actividad 4
Problemas de aplicación
⏱️ Subsección 1.3: Elementos No Visibles
Período, Frecuencia y Velocidad de Propagación
📝 Actividad 2: Dibujo y Análisis de Ondas
📐 Instrucción para dibujo:
En tu cuaderno: Dibuja una onda transversal de 4 ciclos con:
• Longitud de onda (λ) = 6 metros
• Amplitud (A) = 3 metros
• La onda demora 48 segundos desde el inicio hasta el final
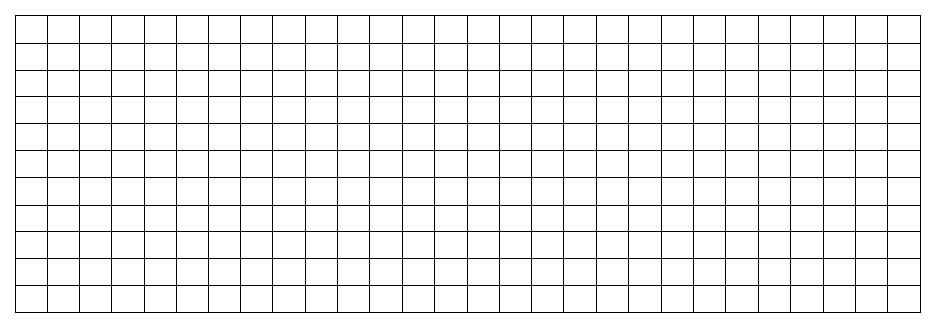
📏 Cada cuadrado mide 1m de arista
📊 Preguntas basadas en tu dibujo:
🎵 Pregunta 2:
✅ Desarrollo - Pregunta a)
📋 Pregunta:
¿Cuál es el periodo de la onda?
📊 Datos:
- Número de ciclos: 4 ciclos
- Tiempo total: 48 segundos
📖 Concepto:
El periodo (T) es el tiempo que demora la onda en completar un ciclo completo. Se calcula dividiendo el tiempo total entre el número de ciclos completados.
🔢 Paso 1: Identificar la fórmula
La fórmula general para calcular el periodo es:
donde T es el periodo en segundos
🔢 Paso 2: Sustituir los valores conocidos
Reemplazamos los datos del problema:
El periodo es de 12 segundos por ciclo
Esto significa que la onda tarda 12 segundos en completar una oscilación completa.
✅ Desarrollo - Pregunta b)
📋 Pregunta:
¿Cuál es la frecuencia de la onda?
📊 Datos:
- Periodo (T): 12 segundos (calculado en la pregunta anterior)
📖 Concepto:
La frecuencia (f) es el número de ciclos completos que realiza la onda por segundo. Es la inversa del periodo, es decir, \[f = \frac{1}{T}\].
🔢 Paso 1: Identificar la fórmula
La relación entre frecuencia y periodo es:
También se puede expresar como: \[f = \frac{1}{12}\,\text{Hz}\]
Esto significa que la onda completa aproximadamente 0.0833 ciclos por segundo.
✅ Desarrollo - Pregunta c)
📋 Pregunta:
¿Cuál es su velocidad de propagación?
📊 Datos:
- Longitud de onda (λ): 6 metros
- Frecuencia (f): 0.0833 Hz o 1/12 Hz
📖 Concepto:
La velocidad de propagación (v) es la rapidez con la que se desplaza la onda por el medio. Se relaciona con la longitud de onda y la frecuencia mediante la fórmula fundamental de ondas.
🔢 Paso 1: Identificar la fórmula
La velocidad de propagación se calcula como:
donde \[\lambda\] es la longitud de onda y \[f\] es la frecuencia
🔢 Paso 2: Sustituir los valores conocidos
Reemplazamos \[\lambda = 6\,\text{m}\] y \[f = \frac{1}{12}\,\text{Hz}\]:
Recordemos que \[\text{Hz} = \frac{1}{\text{s}}\], por lo que \[\text{m} \cdot \text{Hz} = \text{m/s}\]
Esto significa que la onda se desplaza a medio metro por segundo (50 cm/s).
✅ Desarrollo - Pregunta d)
📋 Pregunta:
¿Qué valor tiene la distancia de una cresta a otra consecutiva?
📊 Datos:
- Longitud de onda (λ): 6 metros (dato del enunciado)
📖 Concepto:
La distancia entre dos crestas consecutivas (o dos valles consecutivos) se llama longitud de onda (λ). Esta es una propiedad fundamental de las ondas.
🔍 Explicación Visual:
En una onda transversal:
- Cresta: El punto más alto de la onda
- Valle: El punto más bajo de la onda
- Longitud de onda (λ): La distancia entre dos crestas consecutivas (o dos valles consecutivos)
Cresta → Valle → Cresta = 1 longitud de onda (λ)
🔢 Desarrollo:
Por definición, la distancia entre dos crestas consecutivas es igual a la longitud de onda:
Del enunciado sabemos que:
Esta distancia corresponde exactamente a la longitud de onda del problema.
✅ Desarrollo - Pregunta 2
📋 Pregunta:
Un diapasón vibra con una frecuencia de 440 Hz. ¿Cuántas vibraciones ocurren en 1 minuto?
📊 Datos:
- Frecuencia (f): 440 Hz
- Tiempo: 1 minuto
📖 Concepto:
Frecuencia (f) en Hz significa "ciclos por segundo" o "vibraciones por segundo". Si el diapasón vibra a f = 440 Hz, significa que vibra 440 veces en 1 segundo.
🔢 Paso 1: Convertir el tiempo a segundos
Necesitamos trabajar con unidades consistentes:
🔢 Paso 2: Identificar la fórmula
El número de vibraciones se calcula multiplicando la frecuencia por el tiempo:
donde N es el número de vibraciones, f es la frecuencia y t es el tiempo
🔢 Paso 3: Sustituir los valores conocidos
Reemplazamos \[f = 440\,\text{Hz}\] y \[t = 60\,\text{s}\]:
Recordemos que \[\text{Hz} = \frac{1}{\text{s}}\], entonces \[\text{Hz} \cdot \text{s} = 1\]
🔢 Paso 4: Realizar el cálculo
Multiplicamos y simplificamos las unidades:
Las unidades se cancelan: \[\text{Hz} \cdot \text{s} = \frac{1}{\text{s}} \cdot \text{s} = 1\]
¡Esto es más de veintiséis mil vibraciones en solo un minuto!
📊 Actividad 3: Cálculos con Fórmulas
Preguntas sobre Periodo y Frecuencia:
✅ Desarrollo - Pregunta 1
📊 Datos:
- Tiempo para ir y volver (1 ciclo completo): \[t = 1\,\text{s}\]
- Incógnita: \[T = ?\]
📐 Fórmula:
El periodo es el tiempo de un ciclo completo:
🔢 Desarrollo:
✅ Desarrollo - Pregunta 2
📊 Datos:
- Frecuencia: \[f = 0.5\,\text{Hz}\]
- Incógnita: \[T = ?\]
📐 Fórmula:
🔢 Desarrollo:
\[T = \frac{1}{0.5}\,\text{s}\]
\[T = 2\,\text{s}\]
✅ Desarrollo - Pregunta 3
📊 Datos:
- Número de ciclos: \[N = 4\]
- Tiempo total: \[t = 2\,\text{s}\]
- Incógnita: \[f = ?\]
📐 Fórmula:
🔢 Desarrollo:
\[f = 2\,\text{Hz}\]
✅ Desarrollo - Pregunta 4
📊 Datos:
- Frecuencia: \[f = 2\,\text{Hz}\] (calculado en pregunta 3)
- Incógnita: \[T = ?\]
📐 Fórmula:
🔢 Desarrollo:
\[T = 0.5\,\text{s}\]
✅ Desarrollo - Pregunta 5
📊 Datos:
- Número de oscilaciones: \[N = 57\,600\]
- Tiempo total: \[t = 4\,\text{h} = 14\,400\,\text{s}\]
- Incógnita: \[T = ?\]
📐 Fórmula:
🔢 Desarrollo:
\[T = \frac{1}{4}\,\text{s}\]
\[T = 0.25\,\text{s}\]
✅ Desarrollo - Pregunta 6
📊 Datos:
- Tiempo para 1 vuelta completa: \[t = 1\,\text{h} = 3600\,\text{s}\]
- Incógnitas: \[T = ?\], \[f = ?\]
📐 Fórmulas:
Periodo: El tiempo de un ciclo completo
Frecuencia:
🔢 Desarrollo:
Periodo:
Frecuencia:
\[f = \frac{1}{3600}\,\text{Hz}\]
• Periodo: \[T = 3600\,\text{s}\]
• Frecuencia: \[f = \frac{1}{3600}\,\text{Hz}\]
✅ Desarrollo - Pregunta 7
📊 Datos:
- Número de oscilaciones: \[N = 12\]
- Tiempo total: \[t = 4\,\text{s}\]
- Incógnita: \[T = ?\]
📐 Fórmula:
🔢 Desarrollo:
\[T = \frac{1}{3}\,\text{s}\]
\[T = 0.33\,\text{s}\]
✅ Desarrollo - Pregunta 8
📊 Datos:
- Periodo: \[T = 0.025\,\text{s}\]
- Incógnita: \[f = ?\]
📐 Fórmula:
🔢 Desarrollo:
\[f = 40\,\text{Hz}\]
🎯 Actividad 4: Problemas de Aplicación
Problemas de Análisis de Ondas:
📊 Problema 1
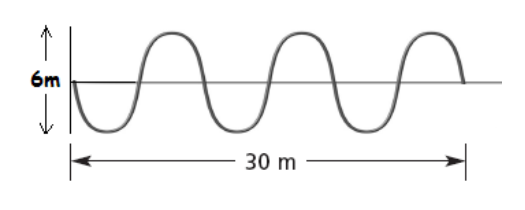
Se observa una onda con las siguientes características:
- Amplitud: 6 metros
- Distancia total: 30 metros
- Número de ciclos completos: 3 ciclos
📊 Problema 2
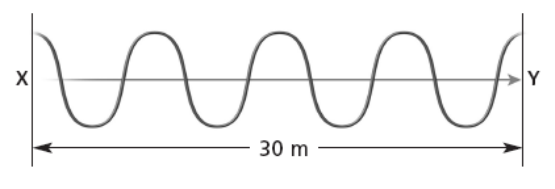
Se observa una onda que tarda 20 segundos en ir de X hasta Y:
- Distancia de X a Y: 30 metros
- Tiempo total: 20 segundos
- Número de ciclos: 4 ciclos
✅ Respuesta - Pregunta 1a

📊 Lo que SÍ podemos decir de la imagen:
✅ Es una representación gráfica típica de onda transversal
- La gráfica muestra desplazamiento perpendicular a la dirección de propagación
- Este tipo de representación se usa convencionalmente para ondas transversales
❌ Lo que NO podemos determinar solo con la imagen:
1. ¿Es mecánica o electromagnética?
❌ IMPOSIBLE saberlo sin contexto adicional
La forma sinusoidal no nos dice nada sobre su naturaleza física. Podría ser cualquiera de las dos.
2. ¿Es realmente transversal o longitudinal?
⚠️ AMBIGUO: Aunque la representación es típica de transversal, las ondas longitudinales (como el sonido) también se grafican así por convención.
En un gráfico de sonido, mostramos "desplazamiento vs posición" aunque físicamente las partículas oscilan paralelas a la propagación, no perpendiculares.
🎯 Ejemplos según el contexto:
| Si el enunciado dijera... | Entonces sería... |
|---|---|
| 🔊 "Onda sonora" | Mecánica y longitudinal |
| 🌍 "Onda S sísmica" | Mecánica y transversal |
| 💡 "Onda luminosa" | Electromagnética y transversal |
| 🪢 "Onda en una cuerda" | Mecánica y transversal |
| 🌊 "Onda en superficie del agua" | Mecánica y transversal |
💡 Conclusión:
Solo con la imagen: FALTA INFORMACIÓN
Para clasificar completamente una onda necesitamos conocer:
- El medio de propagación (o si no hay medio)
- El contexto físico del problema
- La naturaleza de la perturbación
📐 Sobre la representación gráfica:
La representación gráfica es solo una convención matemática para visualizar la oscilación, no refleja necesariamente la dirección real del movimiento de las partículas.
Ejemplo: El sonido (onda longitudinal) se grafica igual que una onda en una cuerda (onda transversal), aunque el movimiento físico de las partículas es completamente diferente.
📝 Respuesta Final
Con solo la imagen podríamos suponer que es transversal (por la convención gráfica), pero NO podemos determinar con certeza si es mecánica/electromagnética ni confirmar si es longitudinal/transversal sin información adicional del contexto físico.
⚠️ Se necesita más información del enunciado
✅ Respuesta - Problema 1b
📋 Pregunta:
¿Cuántos ciclos posee esta onda?
📖 Concepto:
Un ciclo completo es una oscilación completa de la onda, desde cualquier punto hasta que vuelve a la misma posición haciendo el mismo movimiento. Por ejemplo: desde una cresta, pasando por el equilibrio, bajando al valle, y regresando a una cresta.
🔍 Contando los ciclos:
Según los datos del problema:
- Distancia total: 30 metros
- Se observan claramente: 3 crestas completas
- Entre cada par de crestas: hay 1 ciclo completo
La figura comienza con un valle, luego un monte, y esta figura se repite 3 veces, luego hay 3 ondas, o 3 ciclos completos:
La onda completa 3 oscilaciones completas a lo largo de los 30 metros.
✅ Respuesta - Problema 1c
📋 Pregunta:
¿Cuál es el valor de la amplitud de esta onda?
📖 Concepto:
La amplitud (A) es la altura máxima de la onda medida desde el punto de equilibrio (línea media) hasta la cresta (punto más alto) o hasta el valle (punto más bajo).
🔍 Lectura del gráfico:
Según los datos proporcionados en el problema:
- El valor desde el valle al monte está indicado como 6 metros
- Esto significa que desde el centro (equilibrio) hasta la cresta hay 3 metros
- Y desde el centro hasta el valle también hay 3 metros
La altura de la onda desde el punto de equilibrio es de 3 metros.
✅ Respuesta - Problema 1d
📋 Pregunta:
¿Cuál es el valor de su longitud de onda?
📊 Datos:
- Distancia total: 30 metros
- Número de ciclos: 3 ciclos
📖 Concepto:
La longitud de onda (λ) es la distancia que ocupa un ciclo completo de la onda. Es la distancia entre dos puntos equivalentes consecutivos (por ejemplo, de cresta a cresta).
🔢 Paso 1: Identificar la fórmula
🔢 Paso 2: Sustituir valores
🔢 Paso 3: Calcular
Cada ciclo completo de la onda mide 10 metros.
✅ Respuesta - Problema 1e
📋 Pregunta:
¿Qué distancia existe entre una cresta y la cresta siguiente? ¿Y entre un valle y el valle siguiente?
📖 Concepto:
La distancia entre dos puntos equivalentes consecutivos (cresta-cresta o valle-valle) es exactamente la longitud de onda (λ).
🔍 Explicación:
Por definición:
- Cresta a cresta: Es la distancia que ocupa un ciclo completo = λ
- Valle a valle: También es la distancia de un ciclo completo = λ
- Sabemos que λ = 10 metros (calculado en la pregunta anterior)
• Distancia cresta-cresta = 10 metros
• Distancia valle-valle = 10 metros
Ambas distancias son iguales a la longitud de onda (λ = 10 m).
✅ Desarrollo - Problema 2a
📋 Pregunta:
¿Cuál es el período de esta onda, expresado en segundos?
📊 Datos:
- Tiempo total: 20 segundos
- Número de ciclos: 4 ciclos
📖 Concepto:
El periodo (\[T\]) es el tiempo que tarda la onda en completar un ciclo completo. Se calcula dividiendo el tiempo total entre el número de ciclos completados.
🔢 Paso 1: Identificar la fórmula
El periodo se calcula como:
🔢 Paso 2: Sustituir los valores conocidos
Reemplazamos los datos:
🔢 Paso 3: Realizar el cálculo
Dividimos y simplificamos:
\[T = 5.0\,\text{s}\]
La onda tarda aproximadamente 5.0 segundos en completar una oscilación.
✅ Desarrollo - Problema 2b
📋 Pregunta:
¿Cuál es la frecuencia de esta onda, expresada en Hertz?
📊 Datos:
- Periodo (T): 5.0 segundos (calculado en pregunta anterior)
📖 Concepto:
La frecuencia (f) es el número de ciclos por segundo y es la inversa del periodo.
🔢 Paso 1: Identificar la fórmula
La relación entre frecuencia y periodo es:
🔢 Paso 2: Sustituir el valor del periodo
Reemplazamos \[T = 5.0\,\text{s}\]:
🔢 Paso 3: Realizar el cálculo
Calculamos la frecuencia:
\[f = 0.2\,\text{Hz}\]
También se puede expresar como: \[f = \frac{1}{5}\,\text{Hz}\]
La onda completa 0.2 ciclos por segundo.
✅ Desarrollo - Problema 2c
📋 Pregunta:
¿Cuál es su longitud de onda expresada en metros?
📊 Datos:
- Distancia total: 30 metros
- Número de ciclos: 4 ciclos
📖 Concepto:
La longitud de onda λ es la distancia que ocupa un ciclo completo. Se calcula dividiendo la distancia total entre el número de ciclos.
🔢 Paso 1: Identificar la fórmula
La longitud de onda se calcula como:
🔢 Paso 2: Sustituir los valores conocidos
Reemplazamos los datos:
🔢 Paso 3: Realizar el cálculo
Dividimos y simplificamos:
\[\lambda = \frac{15}{2}\,\text{m}\]
\[\lambda = 7.5\,\text{m}\]
Cada ciclo completo mide aproximadamente 7.5 metros.
✅ Desarrollo - Problema 2d
📋 Pregunta:
¿Cuál es la velocidad de propagación de esta onda?
📊 Datos:
- Longitud de onda (λ): 7.5 metros
- Periodo (T): 5 segundos
- Frecuencia (f): 0.2 Hz
- Distancia total: 30 metros
- Tiempo total: 20 segundos
📖 Concepto:
La velocidad de propagación (v) es la rapidez con la que se desplaza la onda. Podemos calcularla usando tres métodos diferentes, todos deben dar el mismo resultado:
🔢 Método 1: Usando \[v = \frac{\lambda}{T}\]
Relaciona la longitud de onda con el periodo:
Sustituyendo los valores conocidos:
Realizando el cálculo:
\[v = 1.50\,\text{m/s}\]
🔢 Método 2: Usando \[v = \lambda \times f\]
Relaciona la longitud de onda con la frecuencia:
Sustituyendo los valores conocidos:
Realizando el cálculo (recordando que \[\text{Hz} = \frac{1}{\text{s}}\]):
\[v = 1.5\,\text{m/s} = 1.50\,\text{m/s} \,\checkmark\]
🔢 Método 3: Usando \[v = \frac{d}{t}\]
Usando la fórmula básica de velocidad (distancia entre tiempo):
Sustituyendo los valores conocidos:
Realizando el cálculo:
\[v = \frac{3}{2}\,\text{m/s}\]
\[v = 1.50\,\text{m/s} \,\checkmark\]
La onda recorre 30 metros en 20 segundos.
La onda se desplaza a 1.50 metros por segundo.
🎯 ¿Cuándo usar cada método?
- Método 1 \[v = \frac{\lambda}{T}\]: Cuando conoces la longitud de onda y el periodo
- Método 2 \[v = \lambda \times f\]: Cuando conoces la longitud de onda y la frecuencia
- Método 3 \[v = \frac{d}{t}\]: Cuando conoces la distancia total recorrida y el tiempo total
Importante: En problemas de ondas, siempre es útil verificar tu respuesta usando un método alternativo cuando sea posible.
Relación entre métodos: Como \[f = \frac{1}{T}\], entonces \[v = \lambda \times f = \lambda \times \frac{1}{T} = \frac{\lambda}{T}\], lo que muestra que los métodos 1 y 2 son equivalentes.