Ejercicios Cromer Calor
Listado de Ejercicios Cromer
Capítulo 11: Calor

1. Hallar la cantidad de calor, en joules y kilocalorías, necesaria para elevar desde 22 hasta 85°C la temperatura de 650 g de agua.

2. (a) ¿Cuánto se eleva la temperatura de 1,25 kg de agua si se le suministran 2×10⁵ J de calor? (b) ¿Cuánto se eleva la temperatura de 750 g de etanol al añadirle 35 kcal de calor?

3. Una piedra de 0,4 kg cae desde 1200 m en un balde que contiene 2,5 kg de agua. ¿Cuánto se eleva la temperatura del agua?

4. En un artículo publicado en 1845, Joule mencionó que la temperatura del agua en el fondo de las cataratas del Niágara es mayor que en la parte alta debido a la conversión de energía mecánica en calor. Suponiendo que las cataratas tienen 50 m de altura, ¿cuál es la elevación de temperatura?

5. ¿Cuál es la capacidad calorífica de una olla de aluminio de 350 g?

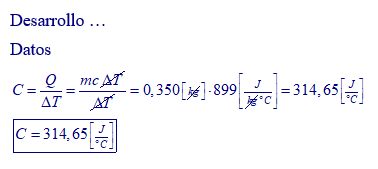
6. ¿Cuánto calor se necesita para elevar en 5 °C la temperatura de 15 kg de granito?

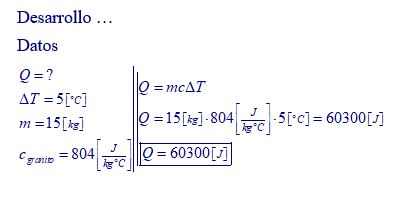
7. Se dispone de 880 J para elevar la temperatura de 350 g de plomo desde 0 a 20°C. ¿Cuál es el calor específico del plomo?

8. ¿Cuál es la capacidad calorífica de un sistema que consta de 7,5 kg de agua en un balde de aluminio de 0,75 kg?

9. Una tetera de aluminio de 400 g contiene 2 kg de agua a 15 °C. ¿Cuánto calor se requiere para elevar la temperatura del agua (y de la tetera) hasta 100 °C?

10. El recipiente interior de un calorímetro contiene 100 g de triclorometano a 35 °C. El recipiente está rodeado de 1,75 kg de agua a 18 °C. Transcurrido un cierto tiempo el triclorometano y el agua alcanzan la temperatura común de 18,22 °C. ¿Cuál es el calor específico del triclorometano?

11. La evaporación de 50 g de triclorometano (cloroformo), CHCl3, de la vasija interior de un calorímetro hacen bajar la temperatura de los 1,6 kg de agua que rodean la vasija en 1,9 °C. ¿Cuál es el calor de vaporización del triclorometano?

12. ¿Cuántos grados desciende la temperatura de los 2,3 kg de agua que rodean la vasija interior de un calorímetro, de la que se han evaporado 65 g de cloroetano, C2H5Cl?

13. Un clavo de hierro de 20 g está siendo golpeado por un martillo de 0,45 kg (1 lb). La velocidad del martillo cuando choca con el clavo es de 9 m/s. Si la mitad de la energía cinética del martillo se convierte en energía térmica del clavo, ¿cuántas veces debe golpearse para elevar su temperatura 25 °C?

14. La capacidad calorífica molar es la capacidad calorífica de 1 mol de sustancia. Calcular las capacidades caloríficas molares (a presión constante) del dióxido de carbono, CO2 oxígeno, O2, y nitrógeno, N2.

15. Se puede demostrar que la capacidad calorífica molar (a presión constante) de un gas ideal diatómico es 7/2 de R, donde R = 8,32 J/K es la constante de los gases. Comprobar esto para (a) el oxígeno y (b) el nitrógeno (ver Prob. 14).

16. La ley de Dulong y Petit dice que las capacidades caloríficas molares de los elementos sólidos son aproximadamente iguales. Comprobar esta ley para el aluminio, cobre y hierro.
OBSERVACIÓN. Esta «ley» era empleada en el siglo XIX para determinar la masa atómica de un elemento a partir de la medida de su calor específico.

17. ¿Cuál es la masa atómica de un elemento cuyo calor específico es 129 J/kg × K? (Ver Prob. 16 y la observación subsiguiente.)

18. Un mol de oxígeno se calienta a una presión constante de 1 atm desde 10 hasta 25°C. (a) ¿Cuánto calor absorbe el gas? (b) Utilizando la ley de los gases ideales, calcular la variación de volumen que experimenta el gas en este proceso. (c) ¿Cuál es el trabajo realizado por el gas durante esta expansión? (d) Calcular, a partir de la primera ley, la variación de energía del gas en este proceso. (e) ¿Cuál es la capacidad calorífica Cv de 1 mol de oxígeno a volumen constante? (f) ¿Cuál es la diferencia Cp – Cv entre las capacidades caloríficas molares a presión constante y a volumen constante?
OBSERVACIÓN. Obsérvese que Cp – Cv es igual a la constante R de los gases. Se puede demostrar que éste es un resultado general para cualquier gas ideal sin más que repetir el problema anterior empleando símbolos algebraicos en lugar de números.

19. Uno de los extremos de una barra de aluminio se mantiene a 220 °C mientras que el otro se mantiene a 0 °C. La barrea tiene 2 m de largo y 1 cm de diámetro. ¿Cuál es la velocidad de conducción del calor a lo largo de la barra?

20. ¿Cuál es la velocidad de transmisión del calor a través de una lámina de 1,2 por 2,4 m y 8 cm de espesor de material aislante cuando una cara está a 22 °C y la otra a 4 °C?

21. El área de la superficie exterior de una casa (paredes y tejado) tiene 280 m², de los cuales 30 m² corresponden a ventanas. Las ventanas tienen un espesor de 0,5 cm, y las paredes y tejado están cubiertas con un material aislante de 8 cm de espesor. Cuando la temperatura exterior es –10 °C, el interior de las ventanas está a 3 °C y el interior de las paredes y techo está a 15 °C. ¿Cuáles son las velocidades de conducción del calor a través de (a) las paredes y tejado y (b) las ventanas?

22. ¿Qué espesor de tejido graso corporal es equivalente en aislamiento a 3 mm de aire?

23. Un radiador con una superficie exterior de 1,5 m² está revestido con pintura de aluminio (e = 0,55). (a) ¿A qué velocidad emite radiación el radiador cuando su temperatura es 50 °C? (b) ¿A qué velocidad es absorbida la radiación por el radiador cuando las paredes de la habitación están a 22 °C? (c) ¿Cuál es la velocidad neta de la radiación procedente del radiador?

24. Demostrar que cuando la diferencia ΔT = Te – Ta entre la temperatura Te de un objeto y la temperatura Ta de las paredes de su recipiente es pequeña comparada con Ta, la velocidad neta de transmisión del calor por radiación del objeto a las paredes puede escribirse R = AεσT_a³ΔT.
OBSERVACIÓN. La ley de Newton del enfriamiento establece que la velocidad de pérdida de calor de un objeto es proporcional a la diferencia ΔT entre las temperaturas del objeto y de su medio circundante. La Ec. 11.12 muestra que la conducción es proporcional a ΔT. El Prob. 24 muestra que la radiación es también proporcional a ΔT, siempre que ΔT sea pequeño comparado con la temperatura del medio.

25. Una esfera de aluminio de 5 cm de diámetro está suspendida por un hilo fino dentro de un tarro en el que se ha hecho el vacío, de modo que sólo puede perder calor por radiación. La temperatura inicial de la esfera es 100 °C, y la pared del tarro está siempre a 22 °C. La emisividad del aluminio es 0,11. (a) ¿Cuál es la velocidad neta inicial de pérdida de calor de la esfera? (b) A la velocidad del apartado (a), ¿cuánto tardará la esfera en pasar de 100° a 90 °C? (c) ¿Cuál es la velocidad neta de pérdida de calor a 90 °C? (d) A la velocidad del apartado (c), ¿cuánto tardará la esfera en pasar de 90 a 80 °C? (Sugerencia: Emplear las tablas 7.2 y 11.1 para calcular la capacidad calorífica de la esfera).

26. La temperatura de un filamento de bombilla es 2700 K e irradia energía a la velocidad de 100 W. Si la emisividad del filamento es 0,42, ¿cuál es su área?

27. Durante el ejercicio físico la sangre a 37,0 °C fluye a la piel a la velocidad de 100 g/s. Si la velocidad de transmisión del calor en la etapa 1 es 500 W, ¿cuál es la temperatura de la sangre cuando vuelve al interior del cuerpo, suponiendo que todo el calor transmitido procede de la sangre y que el calor específico de ésta es igual al del agua?

28. Una persona no habituada al clima tropical puede producir un máximo de 1,5 kg de sudor por hora. ¿Cuál es la velocidad máxima de pérdida de calor por evaporación de esa persona?