Espejos
En la figura se observa la formación de una imagen en un espejo plano.
la distancia p es la distancia del objeto al espejo (nosotros usaremos la letra o, para referirnos a esta distancia)
la distancia q es la distancia de la imagen al espejo (nosotros usaremos la letra i, para referirnos a esta distancia)
Notar que la imagen se forma por la proyección de los rayos reflejados, cuando esto ocurre la imagen se llama virtual, y se encuentra en la mayoría de los casos detrás del espejo.
En un espejo plano, la imagen tiene tres propiedades ...
- La imagen es derecha
- La imagen es del mismo tamaño que el objeto
- La imagen está a la misma distancia del espejo como el objeto lo está del espejo. (la distancia imagen y la distancia objeto son iguales)

En al figura una mujer está de pie delante de un espejo plano.
Cuál es la mínima altura del espejo para que ella se vea de cuerpo completo.
a)igual a su altura
b) igual a la mitad de su altura.
envía tu respuesta con el desarrollo al correo [email protected]
La siguiente expresión se llama aumento lateral, indica cuantas veces la imagen es más grande o más pequeña que el objeto.
Si M es mayor que 1 vamos a decir que la imagen es ampliada, y si M es menor que 1, diremos que la imagen es reducida.
Espejos Esféricos
El tipo más común de espejo curvo es un espejo esférico. Como muestra la Figura de la izquierda, un espejo esférico tiene la forma de una sección de la superficie de una esfera hueca.

Si se pule la superficie interior del espejo, es un espejo cóncavo.
Si la superficie exterior se pule, es un espejo convexo.
El dibujo muestra dos tipos de espejos, con un rayo de luz que se refleja desde la superficie pulida.
La ley de la reflexión se aplica, tal como lo hace en un espejo plano.
En un espejo curvo, los rayos paralelos convergen en el foco. la distancia desde el vértice del espejo al foco se llama distancia focal y es siempre igual a la mitad del radio del espejo esférico.
En un espejo cóncavo, el centro de curvatura está delante del espejo, y el foco también, luego el radio y el foco de este espejo tienen signo positivo.
En un espejo convexo, el centro de curvatura está a la derecha del espejo, y el foco también, luego el radio y el foco de este espejo tienen signo negativo.
Todo lo que está delante del espejo (del mismo lado de donde viene la luz) tiene signo positivo.
Todo lo que esté detrás del espejo (del lado opuesto de donde viene la luz) tiene signo negativo.
Espejos Cóncavos
Los espejos, se estudian usando el trazado de rayos, y para esto es necesario definir algunas propiedades de los espejos, como es el eje principal, el centro de curvatura y el vértice (V).
En la figura anterior se puede observar que todos los rayos paralelos al eje principal convergen en un mismo punto, que se llama punto focal, y este punto se encuentra a una distancia del vértice del espejo llamado distancia focal, que es exactamente igual a la mitad del radio de curvatura del espejo.
Si usamos un poco de geometría con la figura anterior, y observamos los triángulos semejantes que se formanm, podemos concluir que la razón entre las alturas h' y h, es igual a la razón entre las bases q y p, como los triángulos están invertidos, se usa el signo menos. (recordar que nosotros usaremos las letras i para la distancia imagen y o para la distancia objeto, luego M = -i/o)
Trazado de Rayos
Para hallar la imagen son suficientes dos rayos, pero siempre hay que dibujar tres.
estos son:
El rayo paralelo, que se desvía hacia el foco del espejo.
El rayo que pasa por el foco, que se desvía paralelo.
y el rayo que pasa por el centro de curvatura, que no se desvía, y regresa por el mismo camino del rayo incidente.
Aquí podemos ver los tres rayos que emergen de un mismo objeto y la intersección de los rayos reflejados forma la imagen.
Notar que el objeto se encuentra a una distancia mayor a la distancia focal, cuando esto ocurre la imagen siempre será real e invertida, y el tamaño de la imagen va a depender de la distancia a la que se halle del foco.
Cuando el objeto se ubica entre el foco y el centro de curvatura del espejo, la imagen siempre será virtual, derecha y ampliada.

En forma analítica se puede hallar la imagen usando la ley de Gauss
![]()
Ejemplo
Un espejo esférico tiene una distancia focal de +10.0 cm.
a) Ubique y describa la imagen para una distancia de objeto de 25.0 cm.
i = (f-1-o-1)-1 = (10-1-25-1)-1=16,67cm
m=-i/o = -16,67/25=-0,67
luego la imagen es real, ya que i > 0 (el signo de i, indica si la imagen es real o virtual)
la magen es invertida, ya que m<0 (el signo del aumento indica si la inmagen es derecha o invertida)
la imagen es reducida, ya que \m\ <1 (el valor absoluto de m indica si la imagen es ampliada o redeucida)
b) Ubique y describa la imagen para una distancia de objeto de 10.0 cm.
si el objeto está ubicado en el foco del espejo, entonces la imagen se encuentra en el infinito.
Como infinito no es un número, no sepuede describir la imagen.
c) Ubique y describa la imagen para una distancia de objeto de 5.00 cm.
i = (f-1-o-1)-1 = (10-1-5-1)-1=-10cm
m=-i/o = -(-10)/5=+2
luego la imagen es virtual, ya que i < 0 (el signo de i, indica si la imagen es real o virtual)
la magen es derecha, ya que m>0 (el signo del aumento indica si la inmagen es derecha o invertida)
la imagen es ampliada, ya que \m\ >1 (el valor absoluto de m indica si la imagen es ampliada o redeucida)

EJEMPLO 36.4 Imagen formada por un espejo convexo
Un espejo retrovisor, como se muestra en la figura, muestra
la imagen de un camión ubicado a 10.0 m del espejo. La distancia
focal del espejo es -0.60 m.
a) Encuentre la posición de la imagen del camión.
i = (f-1-o-1)-1 = (-0.60-1-10-1)-1=-0.57m
m=-i/o = -(-0.57)/10=+0.0566
luego la imagen es virtual, ya que i < 0 (el signo de i, indica si la imagen es real o virtual)
la magen es derecha, ya que m>0 (el signo del aumento indica si la inmagen es derecha o invertida)
la imagen es reducida, ya que \m\ <1 (el valor absoluto de m indica si la imagen es ampliada o redeucida)
Notar que en los espejos convexos la imagen siempre será virtual para los objetos reales
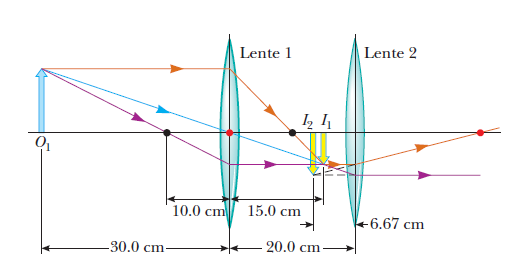
Lentes
La imagen en las lentes se produce por el fenómeno de la refracción de la luz.