Ondas mecánicas
Inicio
Movimiento ondulatorio formado por una gota de agua que cae en un recipiente con agua. Las ondas son capaces de transmitir energía de un lugar a otro como una perturbación, sólo con movimientos
localizados de partículas individuales. En esta unidad estudiamos las propiedades físicas de las
ondas mecánicas.
Objetivos de la clase
- Demostrará por medio de definiciones y ejemplos que ha comprendido el movimiento ondulatorio transversal y longitudinal.
- Definirá, relacionará y aplicará el significado de los términos frecuencia, longitud de onda y rapidez para el movimiento ondulatorio.
- Resolverá problemas en los que intervengan la masa, la longitud, la tensión y la velocidad de onda, en el caso de ondas transversales en una cuerda.
- Escribirá y aplicará una expresión para determinar las frecuencias características en el caso de una cuerda vibrante cuyos extremos están fijos.
Desarrollo
Clase _1
Una onda es una perturbación que viaja por el espacio, además las ondas trasportan energía desde un lugar a otro.
Las ondas se clasifican en Electromagnéticas y Mecánicas y además en Transversales y Longitudinales, las de nuestro interés serán las ondas mecánicas, que son aquellas que necesitan de un medio material para su propagación, si no hay partículas las ondas mecánicas no se pueden propagar.
Una onda en el agua, el sonido, una onda sísmica, son ejemplos de ondas mecánicas.
Tipos de ondas:
Las ondas mecánicas también las podemos clasificar en Transversales y Longitudinales.
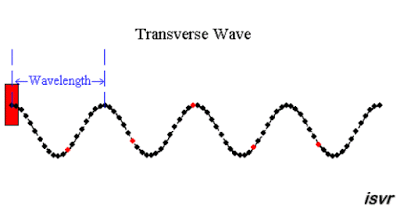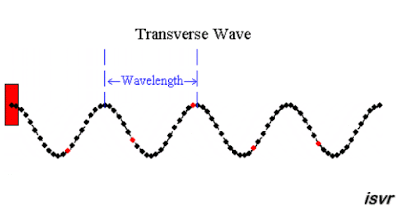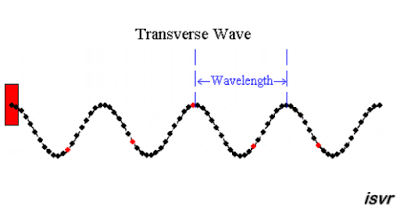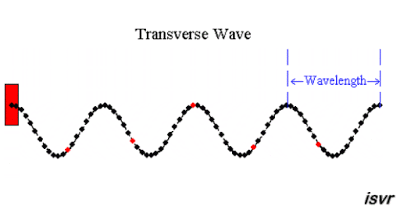
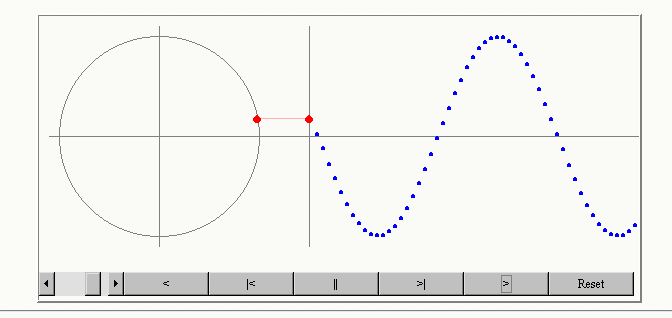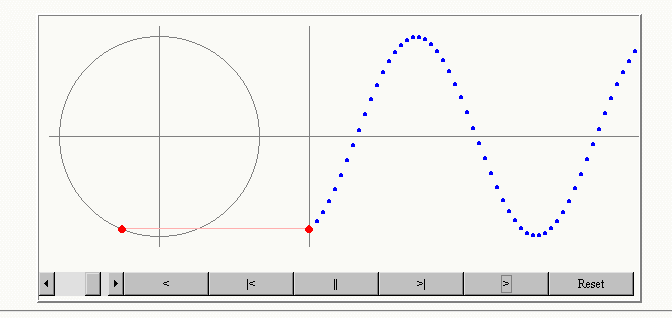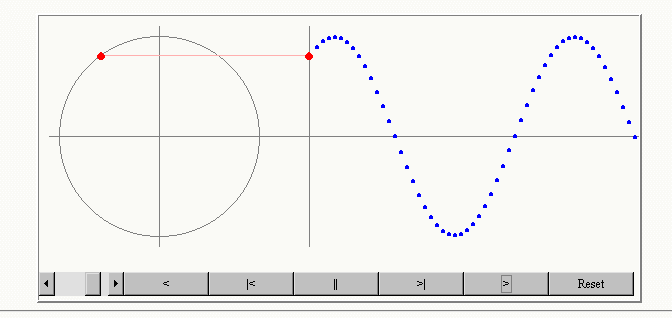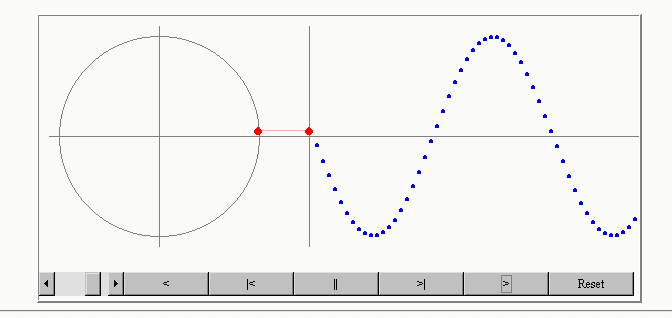
La onda transversal es aquella en donde las partículas del medio se mueven en una dirección perpendicular a la dirección de propagación de la onda.
La onda longitudinal es aquella en donde las partículas del medio se mueven en la misma dirección en la que se propaga la onda.
Una onda se puede caracterizar, con su amplitud, longitud de onda, periodo y frecuencia.
La amplitud (A), es la máxima elevación o depresión de las partículas del medio respecto de la posición de equilibrio.
La longitud de onda (λ) es la distancia que hay entre dos puntos consecutivos de la onda que se encuentran en igualdad de fase. Dos partículas están en fase cuando tienen el mismo desplazamiento y ambas se mueven en la misma dirección. Los montes y los valles son puntos particulares de igualdad de fase.

El periodo (T), es el tiempo que tarda en formarse una onda, o el tiempo que hay entre dos puntos que se encuentran en igualdad de fase.
La frecuencia, es el número de ondas que se forman en la unidad de tiempo.
por lo tanto
frecuencia y periodo son inversamente proporcionales
y ahora podemos definir la velocidad de propagación de una onda.
Notar que esta ecuación, permite calcular la velocidad de propagación, pero se puede caer en el error de creer que la velocidad depende de la frecuencia, longitud de onda o periodo. Siendo que la velocidad de propagación de una onda depende de las características elásticas del medio.
en el caso de una onda que viaja por una cuerda estirada, la velocidad de propagación es ...
donde T es la tensión a la que se somete la cuerda y mu es la densidad lineal de masa
m es la masa de la cuerda, y L es la longitud de la cuerda.