Energía Trabajo y Potencia
Una fuerza realiza trabajo cuando se aplica en la dirección de movimiento

si la fuerza no está en la dirección de movimiento, entonces la componente de la fuerza que está en la dirección de movimiento realiza trabajo.
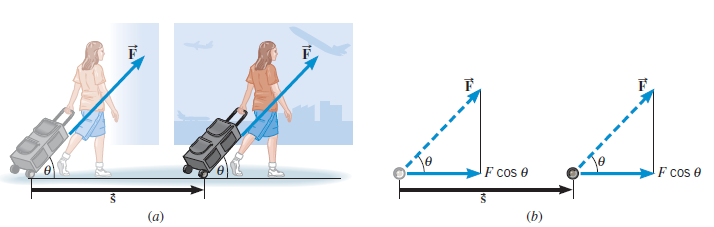
De ahí que trabajo se defina como ...
W = F d cos (θ)
donde θ es el ángulo entre el vector fuerza y el vector desplazamiento.
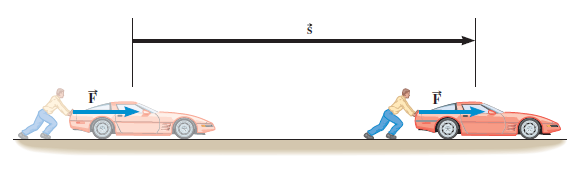
En la siguienten figura la fuerza y el vector desplazamiento forman un ángulo de 0 grados, luego el trabajo es positivo
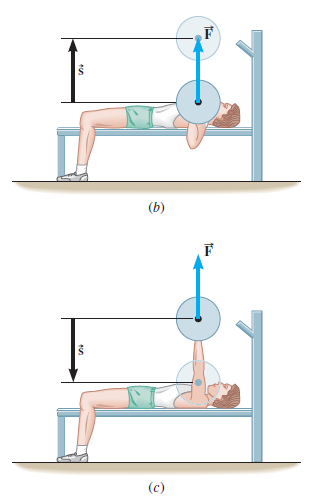
en la figura b el vector fuerza y el vector desplazamiento forman un ángulo de 180°, luego el trabajo es negativo.
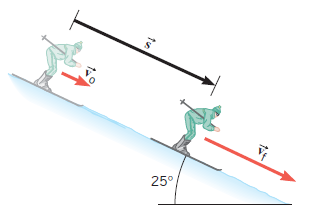
El trabajo mecánico, realizado por la fuerza neta, es igual al cambio en la energía cinética que adquiere el cuerpo.
En la figura, la componente del peso que está en la dirección de movimiento, realiza trabajo, y al mismo tiempo hace que la velocidad del esquiador aumente.
El cambio en la energía cinética es exactamente igual al trabajo realizado por la fierza neta en la dirección de movimiento.
W= ΔK = Kf - Ki
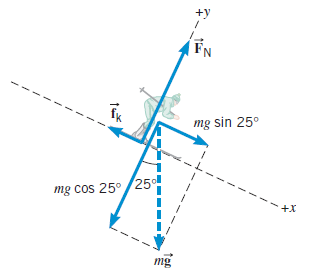
Notar que mg sin 25°, es la componente del peso en la dirección de movimiento.
La energía cinética es la energía que poseen los objetos cuando poseen velocidad, y la energía potencial es la enegía que poseen los cuerpos al estar a cierta altura de un punto de referencia.
Energía Cinética = K = 1/2 mv2
Energía Potencial gravitacional = U = mgh
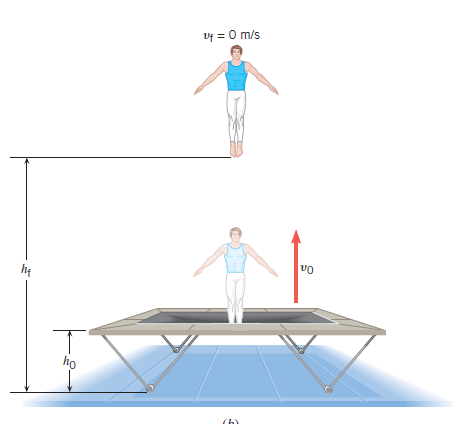
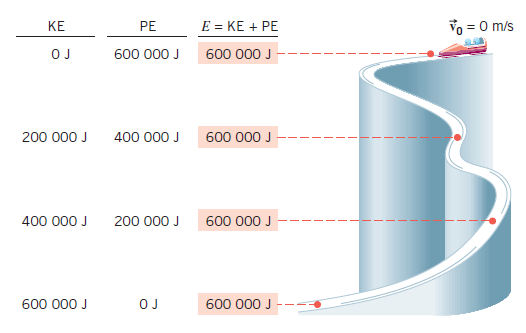
La energía mecáncia es la suma de todas las energías que posee un objeto, esta energía mecánica es la misma en todos los puntos del recorrido.
El motociclista salta una quebrada, tiene una velocidad inicial de 38 m/s, y se encuentra a 70 m sobre el nivel del suelo, al llegar al otro lado de la quebrada aterriza a una altura de 35 m sobre el nivel del suelo, Usando el principio de conservación de la energía mecánica, halle la velocidad que tendrá en este punto.
La Potencia es la rapidez con la que se realiza un trabajo, se mide en Watts.
Cuanto más rápido se realice un trabajo más potencia habrá.
Cuanto más lento se realice un trabajo menos potencia habrá.
Ejercicios
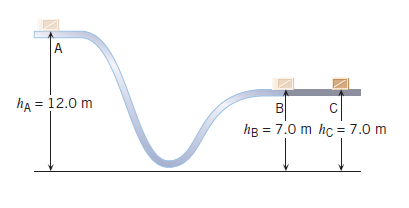
El bloque de la figura en el punto A tiene una velocidad de 5 m/s, entre el A y el punto B no hay roce.
Halle la velocidad con que llega al punto B.
Entre el punto B y C hay roce, el coeficiente de roce cinético en este tramo es de 0,4.
Halle la distancia entre el punto B y el punto C, si el bloque en C se detiene.

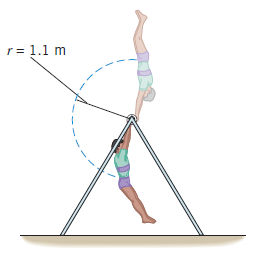


Ejemplo 2. Un ciclista tiene una velocidad de 15 m/s al pie de una colina y una velocidad cie 10 m/s al alcanzar la cumbre de la colina. La masa total del ciclista y la bicicleta es de 65 kg, y la altura vertical de la colina es de 25 m. ¿Cuál es el trabajo aplicado minimo hecho por el ciclista para subir la colina? Si el rendimiento de los músculos del ciclista es de 0,22, ¿cuál es la energía mínima consumida?
Desarrollo:
Primero calculamos los cambios de energía cinética y potencial ...
![]()
![]()
![]()
y, por lo tanto, a partir de la ecuación
![]()
Aqui Delta I es el aumento de energía interna de la bicicleta y el medio debido al rozamiento.
El minimo valor de W es, por lo tanto, 1,18 × 104 J, que es el trabajo que se necesitaria en ausencia de rozamiento.
El rendimiento de una máquina se relaciona con la siguiente ecuación ...

Con un rendimiento de 0,22, la energia mínima necesaria para producir este trabajo es ...
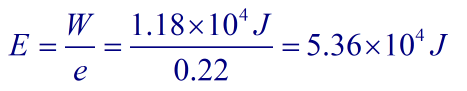
Como en la práctica W tendría que ser mayor que este valor minimo a causa del rozamiento, la energía necesaria sería también mayor.
La potencia P de una máquina es la velocidad a que ésta produce trabajo. Así, si una máquina produce una cantidad de trabajo W en el tiempo t, su potencia es
![]()
Por ejemplo, la potencia de una máquina que produce 75 J de trabajo en 3 s es
![]()
Las unidades de potencia son joules por segundo, o Watts (W) :
![]()
Un kilowatt (kW) Son 1000 watts = 103 Watts.
La velocidad total R de utilización de la energía por parte de una máquina es
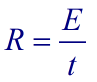
que, puede escribirse como
![]()
En los animales, la velocidad de utilización de la energía se denomina
velocidad metabólica.
Un hombre de 70 kg (154 lb) consume normalmente unos 107 J por día, cantidad ésta que depende de su actividad física, es decir, de la cantidad de trabajo (en el sentido técnico) que hace.
Su velocidad metabólica media es
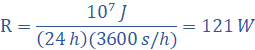
La velocidad metabólica decrece hasta 75 W durante el sueño y se eleva hasta 230 W cuando se camina.
La velocidad metabólica de una persona ocupada en una determinada actividad se mide recogiendo todo el aire que exhala durante 5 min, aproximadamente.
El contenido de oxígeno de este aire se analiza entonces para determinar la cantidad de oxígeno consumido por minuto.
El oxígeno consumido reacciona con hidratos de carbono, grasas y proteínas del cuerpo, liberando una media de 2,0×104 J de energía por cada litro de oxigeno consumido, aproximadamente.
Así, si una persona consume 1,45 litros de oxígeno por minuto durante un rápido pedaleo, su velocidad metabólica es
![]()
Es interesante intentar calcular la velocidad metabólica para una actividad determinada, como el correr. Se ha demostrado que la mayor parte del trabajo efectuado al correr es la aceleración y desaceleración de las piernas a cada paso.
Cuando una pierna se levanta del suelo, se lleva desde el reposo hasta una velocidad aproximdamente igual a la velocidad del cuerpo. En este proceso, los músculos de la pierna efectúan un trabajo igual al cambio de energía cinética de la pierna, es decir, igual a 1/2 mv2, donde m es la masa de la pierna. Así, cuando la pierna se detiene de nuevo, los músculos antagonistas también hacen un trabajo igual a 1/2 mv2.
A cada paso, por lo tanto, los músculos de las piernas hacen un trabajo aproximadamente igual a mv2.
Consideremos un hombre de 70 kg de peso que corre a 3 m/s (10.8 km/h, aproximadamente).
Cada una de sus piernas pesa unos 10 kg, por lo que el trabajo efectuado sobre una pierna a cada paso es
W = mv2 = (10 kg)(3 m/s)2 = 90 J
Supongamos que la longitud de su paso —la distancia entre dos huellas sucesivas del mismo pie— es de 2 m. Entonces el hombre da 1.5 pasos por segundo con cada pierna (usar factor de conversión), de modo que la potencia que actúa sobre sus dos piernas es
P = (2) (90 J/paso) (1.5 pasos/s) = 270 W
como el rendimiento del músculo es solo 0,22, la velocidad de consumo de la energía es
R = P/e = 270 W / 0.22 = 1227.27 W
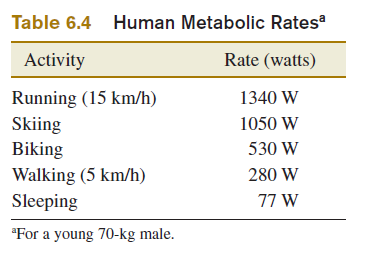
que se aproxima al valor medido de 1340 W, de la Tabla de Ritmo Metabólico