⚡ MRUV: Movimiento Rectilíneo Uniformemente Variado
🎯 Objetivo de la Clase
Comprender y aplicar los conceptos fundamentales del Movimiento Rectilíneo Uniformemente Variado (MRUV), incluyendo sus características, ecuaciones principales y su aplicación en situaciones prácticas, para analizar y resolver problemas relacionados con movimientos acelerados.
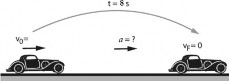
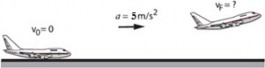
El MRUV es aquel movimiento en trayectoria recta donde la velocidad varía uniformemente, es decir, existe una aceleración constante ($\vec{a} = cte$). La caída de una piedra en vertical o el deslizamiento de unos muchachos por un tobogán o el despegue de un cohete, pueden dar una idea experimental de esta clase de movimientos.
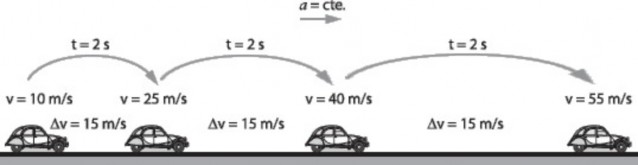
Haz clic en la imagen para ampliar
📋 Características Principales
En este movimiento, el objeto siempre se desplaza con una aceleración constante; por lo tanto sus características principales son:
- A) La aceleración siempre es constante.
- B) La velocidad se incrementa en la misma proporción por cada intervalo de tiempo.
- C) La rapidez y la velocidad media son iguales.
- D) El espacio recorrido en un intervalo de tiempo siempre es mayor que en el intervalo anterior y menor que en el siguiente intervalo.
📐 Ecuaciones del MRUV
Ecuación de Velocidad
$v = v_0 + a \cdot t$
donde: $v$ = velocidad final, $v_0$ = velocidad inicial, $a$ = aceleración, $t$ = tiempo
Nota: Si la velocidad inicial es menor que la velocidad final, entonces se trata de un movimiento con aceleración positiva. Sin embargo, si la velocidad final es menor que la velocidad inicial, entonces se trata de un movimiento con aceleración negativa, es decir, el cuerpo está frenando.
Ecuación de Itinerario
$x = x_0 + v_0 \cdot t + \frac{1}{2} a \cdot t^2$
donde: $x$ = posición final, $x_0$ = posición inicial, $v_0$ = velocidad inicial, $a$ = aceleración, $t$ = tiempo
Ecuación Independiente del Tiempo
$v^2 = v_0^2 + 2a(x - x_0)$
Esta ecuación relaciona la velocidad con la posición sin necesidad de conocer el tiempo. y ($x - x_0$) son equivalentes al desplazamiento.
📚 Actividades de Práctica
Pon en práctica lo aprendido con las siguientes actividades:
📄 Actividad 1
Problemas de MRUV
🔬 Actividad Práctica
Laboratorio de MRUV
📊 Selección Múltiple
Cuestionario de alternativa única
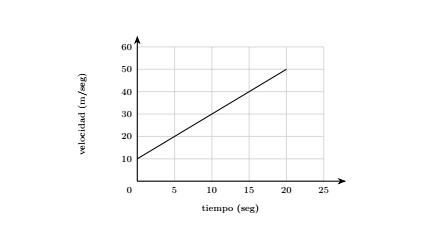
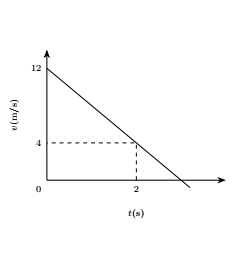
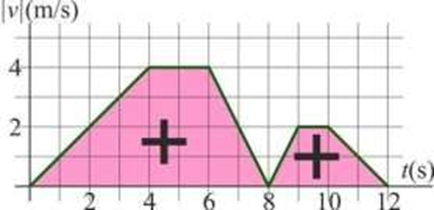
📈 Gráficos MRUV
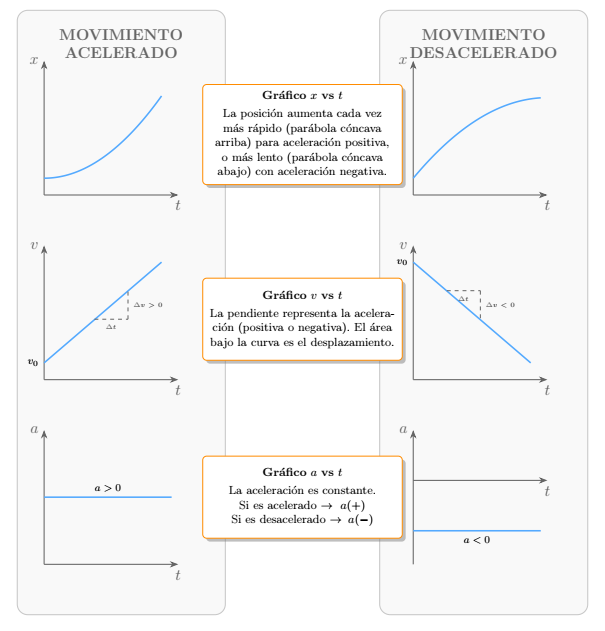
Haz clic en la imagen para ampliar
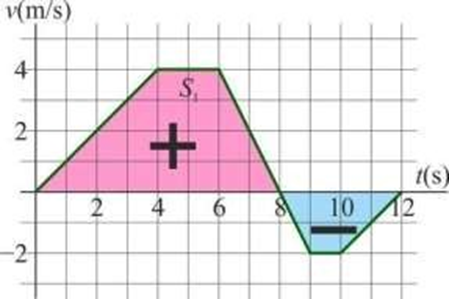
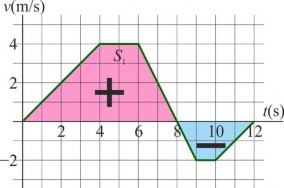
Por ejemplo, en el siguiente gráfico, el móvil estuvo viajando hacia la derecha del sistema de referencia y a partir de los 8 segundos, se movió hacia la izquierda:
📄 Actividad 4
Problemas de gráficos MRUV
🌍 Caída Libre y Lanzamiento Vertical
Caída Libre
Es el movimiento en el cual solamente actúa la fuerza de la gravedad.
Por ejemplo en el movimiento de un paracaidista, además de la fuerza de la gravedad actúa la fuerza de resistencia del aire; por lo tanto su movimiento no es de "caída libre".
De no existir la resistencia del aire, todos los cuerpos caerán con igual aceleración; a esta aceleración se le conoce como "aceleración de gravedad" y se le simboliza con la letra "g".
Su valor varía ligeramente de un lugar a otro de la Tierra y en las cercanías de la superficie terrestre es igual a:
$g = 9.8$ m/s² $\approx 10$ m/s²
Cómo la gravedad apunta verticalmente hacia abajo, le asignaremos el signo menos.
Por lo que la ecuación de Intinerario para el movimiento vertical quedaría de la siguiente manera.
$y(t) = y_0+v_0t-\frac{1}{2}gt^2$
Donde:
- $y(t)$ : Posición vertical final
- $y_0$ : Posición vertical inicial (cuando t =0)
- $v_0$ : Velocidad vertical inicial (si comienza hacia arriba, es positivo. Hacia abajo, negativo).
- g: Aceleración ed gravedad (-10 m/s2) (por eso el signo menos en la ecuación)

📋 Características de la Caída Libre
- No se considera la fuerza de resistencia del aire.(situaciones ideales)
- Tal como en el plano cartesiano, vectores hacia arriba, son positivos. Hacia abajo, son negativos.
- Es un movimiento donde la aceleración es constante e igual a la aceleración de la gravedad.
- En caída libre, si un objeto cae, o se deja caer, o se suelta, la velocidad inical $v_0$ es cero, pero si el objeto se lanza, su velocidad inicial debe ser distinta de cero.
- En cualquier tramo de su trayectoria, el tiempo que tarda en subir es igual al tiempo que tarda en bajar el mismo tramo.
- En cualquier punto de la trayectoria el valor de la rapidez de un cuerpo cuando sube es igual al valor de la rapidez cuando baja el mismo cuerpo.
- En el lanzamiento vertical hacia arriva (LVHA) cuando el cuerpo alcanza el punto más alto, su velocidad es cero, pero su aceleración sigue siendo la aceleración de gravedad. (el movimiento tiene aceleración constante, en ningún punto puede variar)
Importante: Tanto para un movimiento de caída libre, como para LVHA (Lanzamiento Vertical Hacia Arriba), las ecuaciones del MRUA siguen siendo válidas, con la diferencia de que la aceleración siempre será igual a $10$ m/s².
- 1: Ecuación de Itinerario: $y(t) = y_0 + v_0t-\frac{1}{2}gt^2$
- 2: Ecuación de velocidad: $v(t) = v_0 -gt$
- 3: Ecuación Independiente del tiempo: $v^2=v_0^2 - 2g\Delta(x)$
📄 Actividad 5
Problemas de caída libre
📊 Selección de Alternativa Única
Cuestionario de alternativa única