Física 2° Medio
Primer Trimestre - Unidad 1: Cinemática
📐 Cinemática
🎯 Objetivo
Analizar el movimiento rectilíneo uniforme y acelerado de un objeto respecto de un sistema de referencia espacio-temporal, considerando variables como la posición, la velocidad y la aceleración en situaciones cotidianas.
La cinemática es la rama de la física que estudia y describe los movimientos, sin atender a las causas que lo producen. El movimiento es una transformación física en la que cambia la ubicación de un objeto que se denomina móvil.
Para describir el movimiento se necesita un sistema de referencia, un objeto que se supone quieto y parámetros que nos permiten determinar de qué forma cambia de lugar el móvil.
Parámetros que definen el movimiento
- Posición ($\vec{x}$). Es el lugar específico en cierto momento que ocupa el objeto que se mueve respecto al origen de un sistema de referencia. En un movimiento, esta varía de un instante a otro, y es una magnitud vectorial.
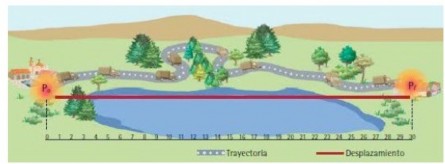
- Trayectoria. Es la línea imaginaria o camino que dibuja el móvil al desplazarse. Puede ser rectilínea, curva, circular, etc..
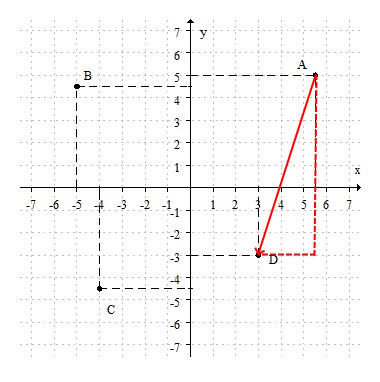
- Desplazamiento ($\Delta \vec{x}$): Es el vector que une la posición inicial con la posición final. Su magnitud es la distancia en línea recta entre estos dos puntos. Se mide en mestros [m] y se determina como: $\Delta \vec{x}=\vec{x_f}-\vec{x_i}$
- Distancia recorrida ($d$). Es la longitud total de la trayectoria recorrida por el móvil. Se mide en metros [m], es una magnitid escalar y siempre es positiva (d$\ge$0).
Haz clic en la imagen para ampliar
💡 Importante
- La distancia ($d$) es igual a la magnitud del desplazamiento (|$\Delta\vec{x}$|) solo si el movimiento es en línea recta y en un solo sentido.
- Si el móvil regresa al punto de partida, su desplazamiento (|$\Delta\vec{x}$|) es cero, pero su distancia recorrida ($d$) es positiva.
📝 Preguntas de análisis
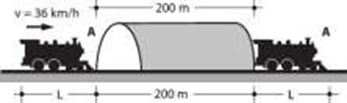
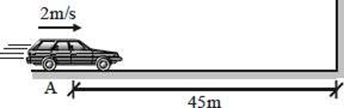
a) ¿Puede la distancia recorrida tener el mismo valor que el desplazamiento? Explica.
b) ¿Puede el desplazamiento tener un valor mayor que la distancia recorrida? Explica.
c) Si el vehículo vuelve al punto de partida, ¿Cuál es el valor de su desplazamiento?
📊 Sistema de Coordenadas: Plano Cartesiano
El Sistema de Coordenadas, también conocido como Sistema de Referencia Cartesiano, es uno de los más empleados para la elaboración de múltiples tipos de gráficos en dos y tres dimensiones.
Haz clic en la imagen para ampliar
📍 Coordenadas Rectangulares
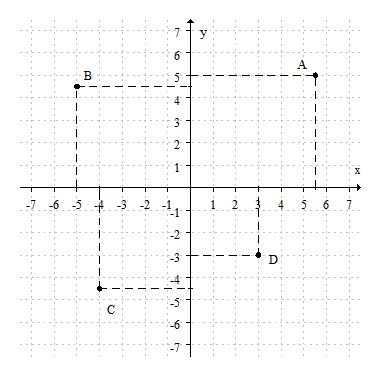
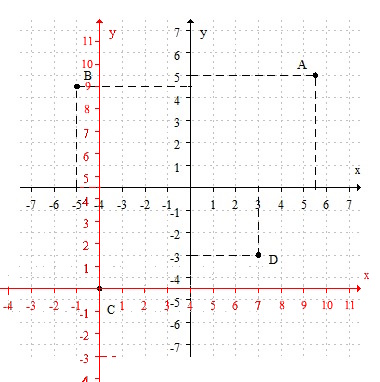
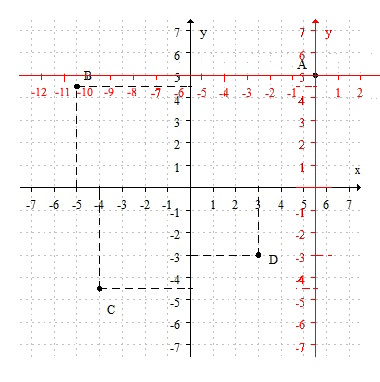
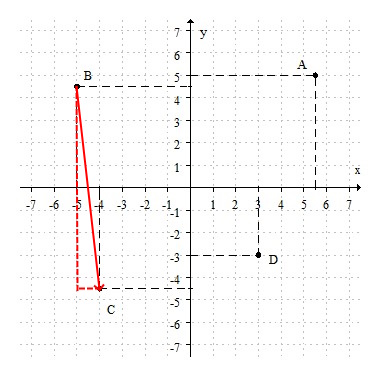
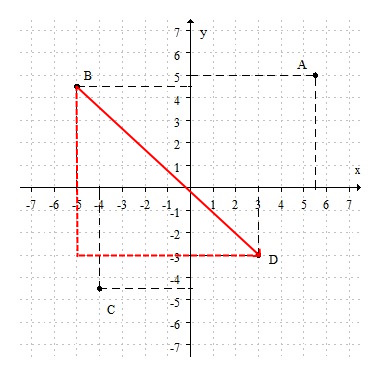
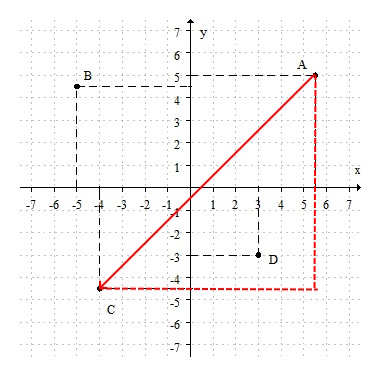
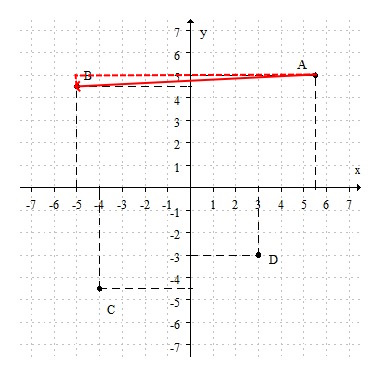
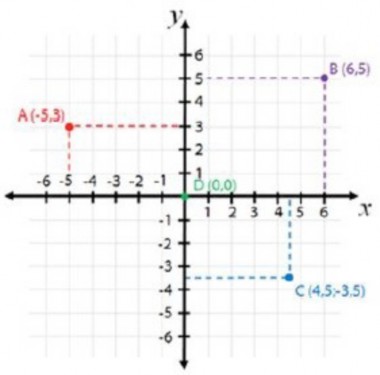
Es la ubicación de un punto en un plano cartesiano. Es decir, en el plano formado por el eje "$x$" (eje horiozontal o eje de las abscisas) y el eje "$y$" (eje vertical o eje de las ordenadas) podemos ubicar un par ordenado $(x, y)$.
Estos valores determinan una coordenada rectangular, llamadas así porque si desde el punto $(x, y)$ trazas una paralela tanto al eje $x$ como al eje $y$ se genera un rectángulo.
📚 Actividades de Práctica
Pon en práctica lo aprendido con las siguientes actividades:
📄 Actividad 1
Problemas de coordenadas
📝 Cuestionario 1
Cuestionario interactivo
⚡ Rapidez y Velocidad
Rapidez y velocidad son dos magnitudes cinemáticas que suelen confundirse con frecuencia.
Recuerda que la distancia recorrida y el desplazamiento efectuado por un móvil son dos magnitudes diferentes.
Haz clic en la imagen para ampliar
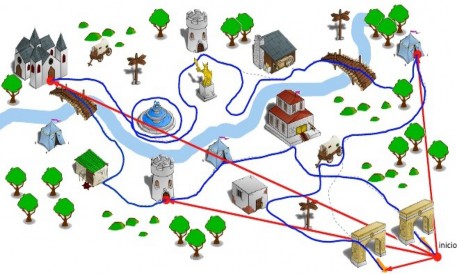
En la figura observamos un laberinto, donde la línea que permite llegar de un punto a otro corresponde a la trayectoria del movimiento (línea azul). Si medimos la longitud de la trayectoria obtenemos la distancia recorrida por el móvil. Sin embargo, la distancia en línea recta (línea roja) desde la posición inicial y la posición final, corresponde al desplazamiento.
Precisamente por eso, cuando las relacionamos con el tiempo, también obtenemos dos magnitudes diferentes.
🚀 Rapidez Media
- Es una magnitud escalar..
- Relaciona la distancia recorrida con el tiempo.
- Siempre es positiva .
$v_m = \frac{d}{t}=\frac{distancia}{tiempo}$
donde $d$ = distancia recorrida
🎯 Velocidad Media
- Es una magnitud vectorial.
- Relaciona el desplazamiento con el tiempo.
- Tiene dirección y sentido.
$\vec{v_m} = \frac{\Delta \vec{x}}{\Delta t}=\frac{\vec{x_f}-\vec{x_i}}{t_f-t-i}$
donde $\Delta x$ = desplazamiento
📏 Unidades
Tanto la rapidez como la velocidad se calculan dividiendo una longitud entre un tiempo, sus unidades también serán el cociente entre unidades de longitud y unidades de tiempo. Por ejemplo:
- m/s (metro por segundo)
- cm/año (centímetro por año)
- km/h (kilómetro por hora)
En el Sistema Internacional de Unidades, la unidad tanto para la rapidez media como para la velocidad media, es el m/s (metro por segundo).
📚 Actividades de Rapidez y Velocidad
Pon en práctica lo aprendido con las siguientes actividades:
🎯 Actividad 2a
Desafío PAES
📄 Actividad 2b
Rapidez y Velocidad
🔄 Actividad 2c
Movimiento Relativo
⏱️ Actividad 2d
Determinar el tiempo
📊 Actividad 2e
Determinar la rapidez y velocidad
📏 Actividad 2f
Determinar Distancias
📈 Actividad 2g
Gráficos de Velocidad